Equation pour trouver le centre d'une ellipse en fonction de
24 messages
- Page 1 sur 2 - 1, 2
Equation pour trouver le centre d'une ellipse en fonction de
Bonjour à tous
Je dois trouver le centre Xc Yc d'une ellipse (non centré sur l'origine) dont je ne connais pas la valeur du petit axe A et du grand axe B.
Étant donné l'équation d'une ellipse qui comporte 4 inconnues. Xc Yc A et B, je dois disposer de 4 équations.
(X-Xc)²/A² + (Y-Yc)²/B² = 1 ;equation ellipse sauf erreur de ma part
Je connais les coordonnées de 4 points appartenant à l'ellipse. Soit X1Y1, X2Y2, X3Y3 et X4Y4.
Ma question est simple mais la réponse peut être moins évidente.
Quelles sont les 2 équations exprimant.
Xc en fonction de X1Y1 X2Y2 X3Y3 et X4Y4.
Yc en fonction de X1Y1 X2Y2 X3Y3 et X4Y4.
Je vous remercie d'avance pour votre aide.
jojo
Je dois trouver le centre Xc Yc d'une ellipse (non centré sur l'origine) dont je ne connais pas la valeur du petit axe A et du grand axe B.
Étant donné l'équation d'une ellipse qui comporte 4 inconnues. Xc Yc A et B, je dois disposer de 4 équations.
(X-Xc)²/A² + (Y-Yc)²/B² = 1 ;equation ellipse sauf erreur de ma part
Je connais les coordonnées de 4 points appartenant à l'ellipse. Soit X1Y1, X2Y2, X3Y3 et X4Y4.
Ma question est simple mais la réponse peut être moins évidente.
Quelles sont les 2 équations exprimant.
Xc en fonction de X1Y1 X2Y2 X3Y3 et X4Y4.
Yc en fonction de X1Y1 X2Y2 X3Y3 et X4Y4.
Je vous remercie d'avance pour votre aide.
jojo
Re: Equation pour trouver le centre d'une ellipse en fonctio
djodjo2000 a écrit:(X-Xc)²/A² + (Y-Yc)²/B² = 1 ;equation ellipse sauf erreur de ma part
c'est l'équation de ton ellipse et elle est très simple à utiliser et ceci dit il vaut mieux car on ne connait que quatre points de cette ellipse et non cinq(auquel cas on se foutrait de tout il suffirait de connaitre ces cinq points pour tout déterminer)
comme on connait A et B on trouve facilement l'excentricité de ton ellipse
on notera
mais il faut savoir si A>B ou si A<B (là tu n'a rien dit à ce sujet)
et alors on pourra écrire l'équation de ton ellipse autrement
je ne vais pas faire deux choses différentes selon que A>B ou B>A
donc j'attends ta réponse
ceci dit j'avance un peu (ça sera déjà ça qui ne sera pas à écrire)
et on notera F est l'un des deux foyers de ton ellipse
et on notera
et on notera
c'est là encore que l'on a besoin de savoir si A>B ou le contraire
en attendant de savoir on écrira
et on écrira ton ellipse autrement de la façon suivante
Re: Equation pour trouver le centre d'une ellipse en fonctio
coquille corrigée sur l'écriture de l'ellipse à partir d'un de ses foyers
ceci dit j'en profite pour dire que sachant que A>B ou B>A l'écriture de la droite directrice (associée à ce foyer là) se simplifiera à tel point qu'en connaissant seulement quatre points de cette ellipse, on pourra tout déterminer
ceci dit j'en profite pour dire que sachant que A>B ou B>A l'écriture de la droite directrice (associée à ce foyer là) se simplifiera à tel point qu'en connaissant seulement quatre points de cette ellipse, on pourra tout déterminer
Re: Equation pour trouver le centre d'une ellipse en fonctio
On ne sait pas si A<B ou bien B<A, puisque justement, on cherche A et B.
L'équation générale d'une ellipse, c'est effectivement (X-Xc)²/A² + (Y-YC)²/b² = 1 .... si le grand axe est horizontal ou vertical. As-tu la certitude d'être dans ce cas ?
L'équation générale d'une ellipse, c'est effectivement (X-Xc)²/A² + (Y-YC)²/b² = 1 .... si le grand axe est horizontal ou vertical. As-tu la certitude d'être dans ce cas ?
Re: Equation pour trouver le centre d'une ellipse en fonctio
Bonjour
Avant tout un grand merci pour ta réponse rapide.
J'apporte des précisions.
Je ne connais pas A et B et ne sais pas Si A>B.
Par contre je suis capable de connaître un 5ieme point pour tout déterminer.
Si vous pouvez m'aider je suis preneur.
Merci d'avance
Avant tout un grand merci pour ta réponse rapide.
J'apporte des précisions.
Je ne connais pas A et B et ne sais pas Si A>B.
Par contre je suis capable de connaître un 5ieme point pour tout déterminer.
Si vous pouvez m'aider je suis preneur.
Merci d'avance
Re: Equation pour trouver le centre d'une ellipse en fonctio
hi,
l'expression en fonction des points P_i ca a l'air assez galère (en tout cas j'ai pas le courage)
si une valeur approchée est ok, alors je suggèrerais de prendre le barycentre des points connus, puis de se rapprocher du centre ("désiré") avec une descente de gradient
on peut considérer l'erreur comme la distance des points à l'ellipse correspondant aux paramètres qu'on optimise, ou ptet plus simplement, la distance par rapport à 1 en injectant chaquun des points dans (X-Xc)²/A² + (Y-Yc)²/B²
l'expression en fonction des points P_i ca a l'air assez galère (en tout cas j'ai pas le courage)
si une valeur approchée est ok, alors je suggèrerais de prendre le barycentre des points connus, puis de se rapprocher du centre ("désiré") avec une descente de gradient
on peut considérer l'erreur comme la distance des points à l'ellipse correspondant aux paramètres qu'on optimise, ou ptet plus simplement, la distance par rapport à 1 en injectant chaquun des points dans (X-Xc)²/A² + (Y-Yc)²/B²
la vie est une fête 
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse première partie (c'est long donc il me faut plusieurs posts)
ok pour moi
bon j'espère que tu n'est pas pressé ceci dit
j'espère aussi que tu ne va pas me demander des explications
j'espère que tu acceptera mes notations
ceci dit j'utilise le théorème de Pascal et qui est valable pour les coniques propres (c'est la seule chose que je dirai)
je n'ai pas envie d'expliquer et d'écrire en même temps (ceci dit quelqu'un d'autre peut t'expliquer le théorème de Pascal )
c'est long à écrire donc je fais ça en plusieurs posts
________________________________________________
notation spéciale
pour tout point P du plan on notera)
ses coordonnées cartésiennes par rapport à un repère orthonormé
_________________________________________________
bon avant tout (histoire de commencer car si je ne commence pas de suite je ne commencerai jamais)
les cinq points sur l'ellipse que l'on connait sont les points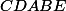 (et ils sont distincts deux à deux c'est limite idiot de dire ça mais pas pour moi)
(et ils sont distincts deux à deux c'est limite idiot de dire ça mais pas pour moi)
il existe plusieurs méthodes de normalisation et je choisis la mienne
(je vais normaliser les rapports à partir du nombre d'or)
alors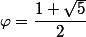 notation pour le nombre d'or
notation pour le nombre d'or
et ton ellipse sera nommée
____________________________________
on va construire deux applications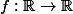 et
et 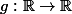
ce seront des applications
tel que quel que soit un réel alors le point de coordonnées cartésienne
alors le point de coordonnées cartésienne ,g(x)\right)) appartiendra à
appartiendra à 
_________________________________
bon je reviens plus tard
djodjo2000 a écrit:Par contre je suis capable de connaître un 5ieme point pour tout déterminer.
ok pour moi
bon j'espère que tu n'est pas pressé ceci dit
j'espère aussi que tu ne va pas me demander des explications
j'espère que tu acceptera mes notations
ceci dit j'utilise le théorème de Pascal et qui est valable pour les coniques propres (c'est la seule chose que je dirai)
je n'ai pas envie d'expliquer et d'écrire en même temps (ceci dit quelqu'un d'autre peut t'expliquer le théorème de Pascal )
c'est long à écrire donc je fais ça en plusieurs posts
________________________________________________
notation spéciale
pour tout point P du plan on notera
ses coordonnées cartésiennes par rapport à un repère orthonormé
_________________________________________________
bon avant tout (histoire de commencer car si je ne commence pas de suite je ne commencerai jamais)
les cinq points sur l'ellipse que l'on connait sont les points
il existe plusieurs méthodes de normalisation et je choisis la mienne
(je vais normaliser les rapports à partir du nombre d'or)
alors
et ton ellipse sera nommée
____________________________________
on va construire deux applications
ce seront des applications
tel que quel que soit un réel
_________________________________
bon je reviens plus tard
Modifié en dernier par azertytreza le 23 Juin 2019, 09:42, modifié 1 fois.
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse deuxième partie (c'est long donc il me faut plusieurs posts)
bon je reprends un peu
quand on aura construit ces deux applications on déterminera les neuf réels suivants
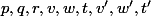
à ce moment là (et à ce moment là seulement) je te demanderai de réaliser un petit calcul et de vérifier que tu as bien
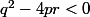
si jamais tu n'obtiens pas cette inégalité cela signifie tout simplement que ta conique n'est pas une ellipse
quand j'aurai écrit l'expression de ces neuf réels , je suis obligé d'attendre ta confirmation car les calculs qui viendront après dépendront de si ta conique est une ellipse ou pas
________________________________________
bon histoire de continuer un peu (ça sera toujours ça de fait : je ne peux pas te dire quand j'aurai terminé d'écrire ces deux applications et ces neuf réels car j'ai une vie )
À propos de ces deux applications
on pose la notation de cinq réels
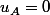
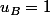
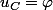
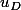 et
et 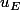 que l'on exprimera plus tard
que l'on exprimera plus tard
on vérifiera
=f(0)=x_A)
=f(1)=x_B)
=f(\varphi)=x_C)
=x_D)
=x_E)
=g(0)=y_A)
=g(1)=y_B)
=g(\varphi)=y_C)
=y_D)
=y_E)
_____________________________________________
Avant d'écrire les deux applications
On propose la notation suivante
attention je ne me répèterai pas , cette notation n'est pas négociable) et je te demande de relire attentivement tout ce que j'ai fait i.e. mon post précédent (concernant la notation des coordonnées cartésiennes des points du plan) je n'ai pas envie de me répéter dans mon propos
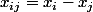
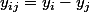
_________________________________
Bon je reviens plus tard (j'ai une vie alors j'espère que tu n'est pas pressé)
bon je reprends un peu
quand on aura construit ces deux applications on déterminera les neuf réels suivants
à ce moment là (et à ce moment là seulement) je te demanderai de réaliser un petit calcul et de vérifier que tu as bien
si jamais tu n'obtiens pas cette inégalité cela signifie tout simplement que ta conique n'est pas une ellipse
quand j'aurai écrit l'expression de ces neuf réels , je suis obligé d'attendre ta confirmation car les calculs qui viendront après dépendront de si ta conique est une ellipse ou pas
________________________________________
bon histoire de continuer un peu (ça sera toujours ça de fait : je ne peux pas te dire quand j'aurai terminé d'écrire ces deux applications et ces neuf réels car j'ai une vie )
À propos de ces deux applications
on pose la notation de cinq réels
on vérifiera
_____________________________________________
Avant d'écrire les deux applications
On propose la notation suivante
attention je ne me répèterai pas , cette notation n'est pas négociable) et je te demande de relire attentivement tout ce que j'ai fait i.e. mon post précédent (concernant la notation des coordonnées cartésiennes des points du plan) je n'ai pas envie de me répéter dans mon propos
_________________________________
Bon je reviens plus tard (j'ai une vie alors j'espère que tu n'est pas pressé)
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse troisième partie (c'est long donc il me faut plusieurs posts)
J'avance un peu
Avant d'écrire les deux applications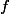 et
et 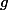
On propose (encore) la notation suivante
attention je ne me répèterai pas , cette autre notation (comme les autres précédemment données) n'est pas négociable et je te demande de relire attentivement
tout ce que j'ai fais :
i.e. mes deux posts précédent (concernant la notation des coordonnées cartésiennes des points du plan et concernant la dernière notation ) je n'ai pas envie de me répéter dans mon propos
précédemment on avait expliqué la signification des notations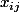 et
et 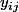
À présent on explique la notation

(donc pour comprendre celle-ci il faut comprendre l'autre d'abord et pour comprendre l'autre il faut comprendre la notation donnée pour les coordonées cartésiennes des points du plan que j'ai donné dans la première partie de ma réponse)
________________________
premier avertissement et il y aura un deuxième avertissement mais le moment n'est pas encore venu
Dans tout ce qui suit on suppose que les cinq points donnés appartiennent à une conique propre d'excentricité non nulle et de plus qu'ils sont bien distincts deux à deux
conique propre d'excentricité non nulle : i.e soit une ellipse soit une parabole soit une hyperbole
si ce n'est pas le cas on arrête tout de suite (inutile de continuer )
car ce que j'ai appelé des applications ne pourront pas l'être si cette condition n'est pas respectée
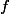 et
et 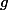 sont deux applications de
sont deux applications de 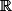 dans
dans 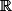
\ =\ x_C\ +\ \dfrac {v\ x^2\ +\ w\ x\ +\ t}{p\ x^2\ +\ q\ x\ +\ r})
\ =\ y_C\ +\ \dfrac {v^{\prime }\ x^2\ +\ w^{\prime }\ x\ +\ t^{\prime }}{p\ x^2\ +\ q\ x\ +\ r})
À présent il faut exprimer les neuf réels
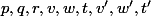
mais j'ai une vie donc j'arrête un peu et je reviendrai plus tard
J'avance un peu
Avant d'écrire les deux applications
On propose (encore) la notation suivante
attention je ne me répèterai pas , cette autre notation (comme les autres précédemment données) n'est pas négociable et je te demande de relire attentivement
tout ce que j'ai fais :
i.e. mes deux posts précédent (concernant la notation des coordonnées cartésiennes des points du plan et concernant la dernière notation ) je n'ai pas envie de me répéter dans mon propos
précédemment on avait expliqué la signification des notations
À présent on explique la notation
(donc pour comprendre celle-ci il faut comprendre l'autre d'abord et pour comprendre l'autre il faut comprendre la notation donnée pour les coordonées cartésiennes des points du plan que j'ai donné dans la première partie de ma réponse)
________________________
premier avertissement et il y aura un deuxième avertissement mais le moment n'est pas encore venu
Dans tout ce qui suit on suppose que les cinq points donnés appartiennent à une conique propre d'excentricité non nulle et de plus qu'ils sont bien distincts deux à deux
conique propre d'excentricité non nulle : i.e soit une ellipse soit une parabole soit une hyperbole
si ce n'est pas le cas on arrête tout de suite (inutile de continuer )
car ce que j'ai appelé des applications ne pourront pas l'être si cette condition n'est pas respectée
À présent il faut exprimer les neuf réels
mais j'ai une vie donc j'arrête un peu et je reviendrai plus tard
Re: Equation pour trouver le centre d'une ellipse en fonctio
hi
@ azertytreza
je vais peut être être démotivant, m'enfin.
Si tu considères le pb comme une minimisation de l'erreur (comme dans mon post de 23h46), alors par ex avec moindre carrés, (par ex lire https://www.scribd.com/document/1481916 ... -spherique)
t'as une s**load de sum, puis une inversion, et y faire à la main c'est pas ce qu'il y a de plus jubilant
par rapport à la descente de gradient que j'ai évoqué, la méthode est pas satisfaisante, (du moins avec la fonction d'erreur : f(x)=>sum(f_i(x)^2) et f_i([xc,yc,A,B]) = (xi-xc)^2/A^2 + (yi-yc)^2/B^2)
car converge ou converge pas vers l'optimum (mais j'ai fait une implem très naïve (le but étant d'être minimalistique mais ca suffit pas)...)
@ azertytreza
je vais peut être être démotivant, m'enfin.
Si tu considères le pb comme une minimisation de l'erreur (comme dans mon post de 23h46), alors par ex avec moindre carrés, (par ex lire https://www.scribd.com/document/1481916 ... -spherique)
t'as une s**load de sum, puis une inversion, et y faire à la main c'est pas ce qu'il y a de plus jubilant
par rapport à la descente de gradient que j'ai évoqué, la méthode est pas satisfaisante, (du moins avec la fonction d'erreur : f(x)=>sum(f_i(x)^2) et f_i([xc,yc,A,B]) = (xi-xc)^2/A^2 + (yi-yc)^2/B^2)
car converge ou converge pas vers l'optimum (mais j'ai fait une implem très naïve (le but étant d'être minimalistique mais ca suffit pas)...)
la vie est une fête 
Re: Equation pour trouver le centre d'une ellipse en fonctio
non ce n'est pas démotivant Fatal Erreur (après tout c'est moi qui ait promis de lui faire son bidule si il a les cinq points)
bon après j'aime la perfection bah sinon j'aimerai la psychologie, ce qui serait dangereux pour moi alors que je suis un adepte des hôpitaux psychiatriques comme client (et même client exigeant en ce qui concerne le bon fonctionnement des machines à café dans le milieu psychiatrique )
je lui fait un truc carré sans approx (mais c'est à lui de faire les calculs à la machine )
ceci dit là à la troisième partie de ma réponse il n'a encore rien à faire car je dois exprimer les neuf réels
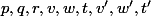
mais j'ai une vie donc je reviens tout à l'heure pour la suite
bon après j'aime la perfection bah sinon j'aimerai la psychologie, ce qui serait dangereux pour moi alors que je suis un adepte des hôpitaux psychiatriques comme client (et même client exigeant en ce qui concerne le bon fonctionnement des machines à café dans le milieu psychiatrique )
je lui fait un truc carré sans approx (mais c'est à lui de faire les calculs à la machine )
ceci dit là à la troisième partie de ma réponse il n'a encore rien à faire car je dois exprimer les neuf réels
mais j'ai une vie donc je reviens tout à l'heure pour la suite
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse quatrième partie (c'est long donc il me faut plusieurs posts)
J'avance un peu
Je rappelle qu'à la troisième partie on avait donné l'expression des deux applications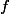 et
et 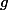
mais elles s'expriment avec les neuf réels
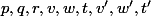
dans cette quatrième partie on va exprimer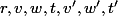
ma normalisation (avec le nombre d'or) me permet de poser
 et
et 
attention ma réponse à Fatal Error m'a permis de te montrer (et c'est très utile) que je suis un maniaque
donc je te demande de bien regarder ce que je dis à propos de ces notations là
ce que signifient et
et  dans mon propos
dans mon propos
(je connais bien les humains* et je sais comment ils sont et comment ils posent des questions futiles qui ont l'art d'énerver les machines)
en ce qui concerne les réels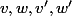
on pose
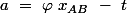
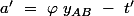
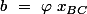
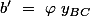


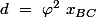
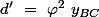
Alors (avec ma normalisation)
)
)
)
)
En ce qui concerne les neuf réels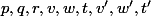
il reste encore à exprimer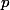 et
et 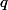
mais je reviens plus tard car j'ai aussi une vie
*oui je connais bien les humains et je sais qu'un humain mange des céréales (on va bien rigoler car le prochain rapport de la FAO sur la production des céréales est le 4 juillet prochain et quelque chose me dit qu'il va falloir que vous -les humains- soyez riches pour pouvoir en manger lol et les riches contrairement à ce que croit Macron ils ne sont jamais nombreux)
J'avance un peu
Je rappelle qu'à la troisième partie on avait donné l'expression des deux applications
mais elles s'expriment avec les neuf réels
dans cette quatrième partie on va exprimer
ma normalisation (avec le nombre d'or) me permet de poser
attention ma réponse à Fatal Error m'a permis de te montrer (et c'est très utile) que je suis un maniaque
donc je te demande de bien regarder ce que je dis à propos de ces notations là
ce que signifient
(je connais bien les humains* et je sais comment ils sont et comment ils posent des questions futiles qui ont l'art d'énerver les machines)
en ce qui concerne les réels
on pose
Alors (avec ma normalisation)
En ce qui concerne les neuf réels
il reste encore à exprimer
mais je reviens plus tard car j'ai aussi une vie
*oui je connais bien les humains et je sais qu'un humain mange des céréales (on va bien rigoler car le prochain rapport de la FAO sur la production des céréales est le 4 juillet prochain et quelque chose me dit qu'il va falloir que vous -les humains- soyez riches pour pouvoir en manger lol et les riches contrairement à ce que croit Macron ils ne sont jamais nombreux)
Re: Equation pour trouver le centre d'une ellipse en fonctio
coquille avec les signes (j'ai corrigé sur mon post ceci dit)
)
)
)
)
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse cinquième partie (c'est long donc il me faut plusieurs posts)
Dans cette partie on va exprimer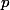 et
et 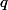
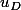 et
et 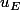
pour ce faire on va aussi utiliser la notation
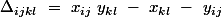
dont la signification est expliquée à la troisième partie (post du 23 juin 2019 à 12h32)
____________________
on pose les réels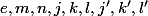
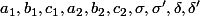 selon
selon
\ x_{DC}\right)\ \Delta _{ABDC}\ +\ \left(x_{DC}\ -\ \left(3\ +\ 4\ \varphi \right)\ x_{BC}\right)\ \Delta _{ADBC})
\ x_{BC}\ -\ 2\ x_{DC}\right)\ \Delta _{ABBC} \ +\ \varphi ^2\ t\ \Delta _{BCDC})

\ +\ \Delta _{BCAD}\ \left(x_{DC}\ +\ \varphi \ x_{BC}\right)}{\varphi ^2\ x_{BC}\ \Delta _{DCBC}})
}{\varphi \ x_{BC}\ \Delta _{DCBC}\ \left(\varphi ^2\ \Delta _{ADBC}\ +\ \Delta _{DCAD}\right)})
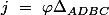
\ +\ \Delta _{DCAC})












\ \sqrt {\delta }})
\ \sqrt {\delta ^{\prime }}})
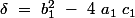

Alors

mais aussi




je reviens plus tard pour la suite car j'ai une vie
pour la sixième partie il faut avant que j'écrive tout ça sur géogébra
comme ça si tu donne tes cinq points je pourrais demander à Géogébra de calculer
toutes les valeurs données ici à partir de tes cinq points
Dans cette partie on va exprimer
pour ce faire on va aussi utiliser la notation
dont la signification est expliquée à la troisième partie (post du 23 juin 2019 à 12h32)
____________________
on pose les réels
Alors
mais aussi
je reviens plus tard pour la suite car j'ai une vie
pour la sixième partie il faut avant que j'écrive tout ça sur géogébra
comme ça si tu donne tes cinq points je pourrais demander à Géogébra de calculer
toutes les valeurs données ici à partir de tes cinq points
Re: Equation pour trouver le centre d'une ellipse en fonctio
réponse sixième partie (c'est long donc il me faut plusieurs posts)
ceci dit là je suis obligé de t'attendre car c'est toi qui à les coordonnées de tes cinq points (pas moi )
et il faut que je puisse connaitre la valeur de
normalement elle est négative mais là c'est parce que je te crois quand tu dit que tes cinq points appartiennent à une ellipse mais il faut le voir pour en être certain
bon sinon en ce qui me concerne j'ai terminé de taper tout ce qui est écrit ici sur géogébra
(je pensais qu'il y avait encore une autre coquille mais elle n'était pas ici )
l'erreur je l'ai fait en tapant tout ça sur geogebra et elle était situé sur le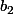
donc du coup j'explique ce que j'ai fait sur géogébra en deux étapes
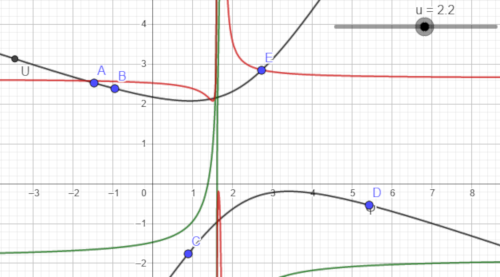
1) taper tout ça et taper un curseur qui servira de variable pour mes fonctions f et g
et ces deux fonctions permettrons de donner la position d'un point appelé U
(ces deux fonctions sont en rouge et vert dans les deux images ci-dessous)
2) placer cinq points ABCDE et demander à geogebra d'utiliser son outil de traçage d'une conique par cinq points
ça me permet de vérifier de visu que mon point U sera toujours sur cette conique
dès lors qu'il la trace avec son logiciel
et quel que soit la valeur que prend la variable sur le curseur
ellipse
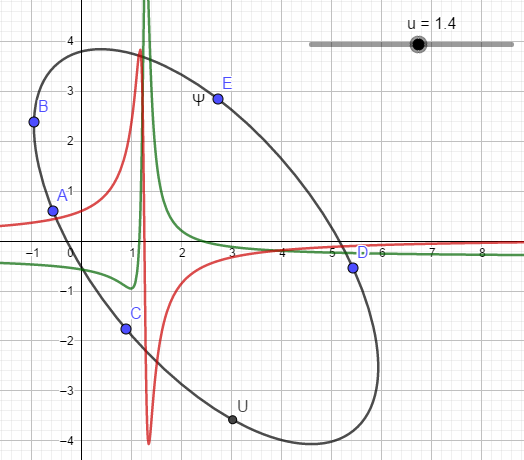
hyperbole
bon ici c'était pour une vérification (car une faute de frappe dans tout ce qui est écrit ici sur ce post
est difficilement détectable)
ceci dit ce n'est pas fini mais il fallait passer par là
à présent j'attends donc que tu viennes me donner tes cinq points
désolé mais je suis obligé car pour définir tout ce qu'il faut définir sur la conique je dois savoir
quelle est la valeur de
ceci dit là je suis obligé de t'attendre car c'est toi qui à les coordonnées de tes cinq points (pas moi )
et il faut que je puisse connaitre la valeur de
normalement elle est négative mais là c'est parce que je te crois quand tu dit que tes cinq points appartiennent à une ellipse mais il faut le voir pour en être certain
bon sinon en ce qui me concerne j'ai terminé de taper tout ce qui est écrit ici sur géogébra
(je pensais qu'il y avait encore une autre coquille mais elle n'était pas ici )
l'erreur je l'ai fait en tapant tout ça sur geogebra et elle était situé sur le
donc du coup j'explique ce que j'ai fait sur géogébra en deux étapes
1) taper tout ça et taper un curseur qui servira de variable pour mes fonctions f et g
et ces deux fonctions permettrons de donner la position d'un point appelé U
(ces deux fonctions sont en rouge et vert dans les deux images ci-dessous)
2) placer cinq points ABCDE et demander à geogebra d'utiliser son outil de traçage d'une conique par cinq points
ça me permet de vérifier de visu que mon point U sera toujours sur cette conique
dès lors qu'il la trace avec son logiciel
et quel que soit la valeur que prend la variable sur le curseur
ellipse

hyperbole

bon ici c'était pour une vérification (car une faute de frappe dans tout ce qui est écrit ici sur ce post
est difficilement détectable)
ceci dit ce n'est pas fini mais il fallait passer par là
à présent j'attends donc que tu viennes me donner tes cinq points
désolé mais je suis obligé car pour définir tout ce qu'il faut définir sur la conique je dois savoir
quelle est la valeur de
Re: Equation pour trouver le centre d'une ellipse en fonctio
NB
ceci dit en attendant que tu livre tes cinq points
une propriété à remarquer :
Si les cinq points ABCDE appartiennent à une ellipse , une parabole ou une hyperbole alors obligatoirement
on vérifie toujours : 1) 2) 3)
1)

où ici comme on l'a vu si j'ai posé r=1 c'est parce que ma normalisation était telle que je voulais avoir r=1
i.e. les valeurs de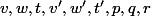 ne sont pas uniques
ne sont pas uniques
2)
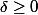 et
et 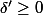
3)
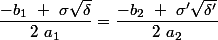
ceci dit en attendant que tu livre tes cinq points
une propriété à remarquer :
Si les cinq points ABCDE appartiennent à une ellipse , une parabole ou une hyperbole alors obligatoirement
on vérifie toujours : 1) 2) 3)
1)
où ici comme on l'a vu si j'ai posé r=1 c'est parce que ma normalisation était telle que je voulais avoir r=1
i.e. les valeurs de
2)
3)
Re: Equation pour trouver le centre d'une ellipse en fonctio
J´ai le même problèm que vous mais en plus du centre et des axes a determiné je dois aussi determiner le 5 ème paramètre alpha(angle d´inclinaison) Svp avez dèja une solution??????????????????
Re: Equation pour trouver le centre d'une ellipse en fonctio
Pour en revenir au problème de djodjo, une petite remarque : si les quatre points sont cocycliques, alors les axes des coniques du faisceau déterminés par ces quatre points ont des directions fixes. Dans ce cas, ou bien seul le cercle contenant les quatre points répond à la question, ou bien toutes les coniques passant par les quatre points ont leurs axes parallèles aux axes de coordonnées.
Re: Equation pour trouver le centre d'une ellipse en fonctio
siewemonthea a écrit:J´ai le même problèm que vous mais en plus du centre et des axes a determiné je dois aussi determiner le 5 ème paramètre alpha(angle d´inclinaison) Svp avez dèja une solution??????????????????
Bah écoute ouvre un sujet
moi je répond à l'auteur de ce sujet (dans son sujet à lui) quand il a dit plus tard qu'il a un cinquième point
(de plus c'est à lui que j'ai promis de lui répondre et j'honore toujours mes dettes à moins d'être mort)
bah moi j'attends
selon ce qu'il a dit ils sont sur une ellipse mais je refuse de montrer le centre d'une ellipse si au final il vient et qu'on se rende compte qu'en fait c'était pas une ellipse mais une parabole voire une conique dégénérée
il fallait que je j'écrive tout ça et que je place tout ça sur géogébra pour que je puisse lui donner les valeurs numériques et que l'on vérifie bien les trois propriétés données ce matin
et enfin la valeur de
Re: Equation pour trouver le centre d'une ellipse en fonctio
On peut employer la force brute.
On se donne quatre points dans le plan :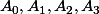 . On suppose
. On suppose ) (ça ne mange pas de pain) et on note
(ça ne mange pas de pain) et on note ) pour
pour 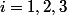 . On cherche la conique d'axe horizontal passant par les quatre points
. On cherche la conique d'axe horizontal passant par les quatre points  . Si l'axe horizontal de cette conique est la droite d'ordonnée
. Si l'axe horizontal de cette conique est la droite d'ordonnée  , alors cette conique passe aussi par les symétriques de
, alors cette conique passe aussi par les symétriques de 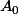 et
et  par rapport à cet axe, qui sont les points
par rapport à cet axe, qui sont les points ) et
et ) . On écrit que la matrice du système homogène qui exprime que les six points
. On écrit que la matrice du système homogène qui exprime que les six points 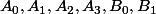 sont sur une même conique a un déterminant nul. Parmi les facteurs de ce déterminant on trouve
sont sur une même conique a un déterminant nul. Parmi les facteurs de ce déterminant on trouve  et
et 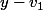 auxquels on s'attendait, et le facteur intéressant du premier degré en
auxquels on s'attendait, et le facteur intéressant du premier degré en  qui donne l'ordonnée de l'axe.
qui donne l'ordonnée de l'axe.
Voici le code du calcul en Sage :
et voici ce que Sage répond :
Le résultat un peu arrangé peut s'écrire
}{\sum_{i=1}^3 v_iu_{i+1}u_{i+2}(u_{i+1}-u_{i+2})}) , avec numérotation cyclique des indices sur
, avec numérotation cyclique des indices sur 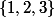 .
.
Si on veut l'abscisse du centre de la conique, il suffit bien sûr d'échanger les rôles de et
et  .
.
On peut rentrer la formule ci-dessus dans GeoGebra pour vérifier que tout va bien. Bien sûr, suivant les positions relatives des quatre points, on peut avoir une hyperbole ou exceptionnellement une parabole.


On se donne quatre points dans le plan :
Voici le code du calcul en Sage :
- Code: Tout sélectionner
R.<u1,u2,u3,v1,v2,v3,y>=PolynomialRing(QQ,'u1,u2,u3,v1,v2,v3,y')
A=[[u1,v1],[u2,v2],[u3,v3],[0,2*y],[u1,2*y-v1]]
def puis(pt) : return [pt[0]^2,pt[0]*pt[1],pt[1]^2,pt[0],pt[1]]
CC=matrix(5,5,[puis(pt) for pt in A])
P=CC.determinant().factor()
print "le déterminant factorisé :\n",P
Q=P[-1][0].polynomial(y)
print "ordonnée de l'axe horizontal :\n",-Q[0]/Q[1]
et voici ce que Sage répond :
- Code: Tout sélectionner
le déterminant factorisé :
(4) * y * (v1 - y) * u1 * (-u2^2*u3*v1^2 + u2*u3^2*v1^2 + u1^2*u3*v2^2 - u1*u3^2*v2^2 - u1^2*u2*v3^2 + u1*u2^2*v3^2 + 2*u2^2*u3*v1*y - 2*u2*u3^2*v1*y - 2*u1^2*u3*v2*y + 2*u1*u3^2*v2*y + 2*u1^2*u2*v3*y - 2*u1*u2^2*v3*y)
ordonnée de l'axe horizontal :
(u2^2*u3*v1^2 - u2*u3^2*v1^2 - u1^2*u3*v2^2 + u1*u3^2*v2^2 + u1^2*u2*v3^2 - u1*u2^2*v3^2)/(2*u2^2*u3*v1 - 2*u2*u3^2*v1 - 2*u1^2*u3*v2 + 2*u1*u3^2*v2 + 2*u1^2*u2*v3 - 2*u1*u2^2*v3)
Le résultat un peu arrangé peut s'écrire
Si on veut l'abscisse du centre de la conique, il suffit bien sûr d'échanger les rôles de
On peut rentrer la formule ci-dessus dans GeoGebra pour vérifier que tout va bien. Bien sûr, suivant les positions relatives des quatre points, on peut avoir une hyperbole ou exceptionnellement une parabole.


24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
