Equation parametrique et suite Suites arithmético-géométriqu

[pyriame]

Bonjour a tous,
Je suis nouveau sur le forum et je viens a votre rencontre pour un problème de math qui , force est de le constater, est en dehors de mes compétences.

C'est une manipulation algébrique que je n'arrive pas a faire.

Je travail sur des équations différentielles biologique dite de Bergmann (pour ceux que cela intéresse
http://www.civilized.com/mlabexamples/glucose.htmld/). Il s'agit bêtement de 3 équations qui s’emboîtent les une dans les autres et forme une boucle. A0 influence Bo qui influence C0 qui influence A1 qui influence B1 etc.. Le tous permet d'obtenir une valeur qui s'’équilibre dans le temps.

L'équation qui m'interesse est de la forme : Gn+1 = Gn + P1(GB-Gn) - Xn.Gn + A avec
-Gn+1= valeur de G au temps n+1
-Gn = valeur de G au temps n
-P1 et GB sont des constantes
-Xn = la valeur d'une autre équation différentielle au temps n.
-A = une valeur fixe introduite uniquement au temps t=0

Pour l’instant je considère que Xn est aussi une constante et qu'ainsi cette équation se résume assez simplement : La valeur de G au temps n +1 est égale a la valeur de G au temps n auquel on ajoute le terme P1(GB-Gn) - Xn.Gn +A (ou A est un reel positif a t= 0 mais = 0 le reste du temps .

Le paramètre sensible pour cette équation est P1 qui permet aux 3 équations différentielle d’être en équilibre, c 'est a dire que pour importe quelle valeur introduite A, au bout d'un certain temps t, la valeur de G redeviens égale à GB. Cette valeur de P1 est obtenu par régression.

Mon problème est le suivant.
Cette équation est valable pour une unité temporelle de 1 min. Soit G0 = valeur de G au temps 0, G1 à une minute, G2 à 2 minutes etc, avec un apport de A au temps t=0.

Je souhaite reformuler mon équation avec comme unité temporelle 1 sec, c'est a dire obtenir la nouvelle valeur de P1 pour qu'en partant de la même valeur G0 et après 60 cycles la valeur g60 soit la même que pour l'équation précédente (=G1) mais avec ici un apport de A/60 à chaque cycle.

En gros plutôt que d'introduire A en une fois au temps 0, je le divise par 60, je l'introduis a chaque cycle et j’obtiens la même valeur final G1 au 60eme passage.

on a donc un couple d'équations:
-En minute et pour la 1ere minute : G1 = G0 + P1 .(GB-G0) - X0.GO + A
- ou reformuler en seconde, pour la 60 ème seconde g60 = g59 + Px(GB-g59) - X0.g59 + A/60
avec G0=g0 et G1=g60.
Je n'arrive pas, connaissant G0 (départ), G1 (arrivé) P1, X0 et GB a trouver Px (le nouveau P1).

J'ai noirci des kilomètre de page et conceptuellement parlant c'est trop ardu pour moi. Les suites j'ai toujours eu du mal : ) Je recherche donc à isoler Px.

Merci par avance de votre aide.

[Ben314]

Salut,
Pour un matheux, un truc du style c'est ce qu'on appelle une suite "arithmético-géométrique", c'est à dire de la forme .
Dans ton cas, on a et .

Une telle suite reste constante égale à ssi c'est à dire .
En retranchant à on obtient ce qui implique que pour tout .
Avec , pour avoir , il faut que c'est à dire

Si j'ai bien compris, là dedans, tu connais tout le monde sauf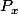 , sauf qu'on ne sait pas résoudre de façon formelle une telle équation (d'inconnue 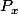), mais on peut bien sûr utiliser des méthodes numériques pour approximer (aussi précisément qu'on veut) cette valeur.
Par exemple par simple dichotomie ou, modulo de vérifier qu'on est dans un contexte favorable, avec un truc style méthode des tangentes de Newton.

[pyriame]

bonsoir et merci beaucoup pour toute ces précisions. C'est exactement la démonstration que je cherchais
Je recherchais effectivement a résoudre formellement l’équation.

Intuitivement et en bonne approximation (qui dérive raisonnablement des valeurs attendu ) se trouve la division par 60. Le fait est que G est une concentration et P1(GB-G0) un flux. Diviser la puissance du flux par 60 (P1/60 et XT/60) donne un résultat qui semble raisonnable. A est absorbé, l'équilibre fini par se faire, seul la courbe des cinétiques est sensiblement différente.

Le coté frustrant c'est que la division porte sur 60 ici mais qu'en réalité ont est sur des battement par minute. l'apport de A doit être divisé par ce nombre de BPM , la division du flux aussi, et qu'il devient très compliquer de vérifier que la dérive a chaque seconde n'est pas proprement catastrophique après 5000 heures et pour des valeur de A variant d'un facteur 1 à 100.

C'est un saut dans l'inconnu !

En tous cas encore merci pour cette aide, ça fait un moment que je tournais autour.