Equation Parametrique

[eugene]

Soit d la droitede representation parametrique

{x=t-1
d {y=-3-t
{z=t

et d' la representation cartesienne

{x=2z
d' {y+z+z=0

dans un repereorthonormal direct (o,i,j,k)

1)determiner un vecteur directeur de d'
2)montrer que d et d' sont non coplanaires.
3)montrer que d et d' possedent une unique perpendiculaire commune , dont on determinera les equations cartesiennes, ainsi une representation parametrique

merci d'avance

[mathelot]

d' la representation cartesienne
{x=2z
d' {y+z+z=0

il semble qu'il y ait une erreur d'énoncé.

[eugene]

d':
|x=2z
|y+z+4=0

non c'est comme ca

[eugene]

d':
|x=2z
|y+z+4=0

non c'est comme ca

[mathelot]

vecteur directeur de d
vecteur directeur de d'
et ne sont pas liés. donc d et d' ne sont pas parallèles.
regardons si d et d' sont sécantes:
les systèmes simultanés d'inconnues t et :



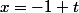
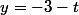
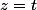
et



impliquent:
0=1
les droites d etd ' ont une intersection vide.
Elles ne sont donc ni parallèles ni sécantes. Elles sont donc non coplanaires.

[eugene]

comment as tu trouver d'

[mathelot]

cherchons une direction orthogonale à et orthogonale à
il vient le système:


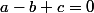
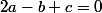
d'où:
a=0 et b=c.
on prend donc
ensuite, j'ai fait à la main mais je soupçonne qu'il y a plus court:
je cherche deux points A et B tels que:


proportionnel à
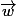
ça me donne le système d'inconnues









on remplace partout les x,y,z par leurs valeurs:



d'où les valeurs de , d'où A, d'où l'équation de la droite (AB)

[mathelot]

je reparamètre (d') en posant z= pour garder des lettres grecques aux paramètres et des lettres latines aux coordonnées.