Equation fonctionnelles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:13
par Dinozzo13 » 18 Juin 2012, 22:13
bonsoir, j'aimerais résoudre l'équation fonctionnelle suivante :
\in\mathbb{R}^2 , f(x\times y)=f(x)\times f(y))
où

désigne un application de

dans

continue.
Je rencontre des problèmes surtout au début.
Voilà, ce que j'ai fait :
Si

alors
=f(x)\times f(0))
,
=0)
ou
=1)
.
Donc
=1)
convient.
Supposons
\neq 1 \forall x \in\mathbb{R})
.
Si
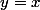
alors
=[f(x)]^2)
;
Si
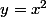
alors
=[f(x)]^3)
;
Je conjecture que pour tout entier naturel
=[f(x)]^n)
.
Mais je ne pense pas que cette conjecture puisse m'aider à trouver la forme
)
.
Or le problème c'est quand je cherche
)
, je trouve
=0)
ou
=1)
.
Et du coup je ne sais pas lequel garder ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:15
par Nightmare » 18 Juin 2012, 22:15
Salut,
pour commencer, as-tu une idée des solutions?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:24
par Dinozzo13 » 18 Juin 2012, 22:24
Bonsoir Nightmare
Nightmare a écrit:Salut,
pour commencer, as-tu une idée des solutions?
Ben, j'ai trouvé
=0, f(x)=1)
et
=x)
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:29
par Nightmare » 18 Juin 2012, 22:29
Tu n'en vois pas d'autres?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:33
par Dinozzo13 » 18 Juin 2012, 22:33
Nightmare a écrit:Tu n'en vois pas d'autres?
J'aurai dit 1/x mais comme

doit être continue sur

...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:34
par Nightmare » 18 Juin 2012, 22:34
Effectivement, et que penses-tu de la fonction carrée?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:38
par Dinozzo13 » 18 Juin 2012, 22:38
Nightmare a écrit:Effectivement, et que penses-tu de la fonction carrée?
Ben alors dans ce cas, toutes les fonctions

conviennent.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:42
par Nightmare » 18 Juin 2012, 22:42
Oui, mais pas que... Que penses-tu de la fonction valeur absolue? Et la fonction
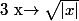
?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:47
par Dinozzo13 » 18 Juin 2012, 22:47
Ouais mais bon, il paraît y en avoir beaucoup.
Les énumérer toutes comme ça sans être sûr de toutes les avoir n'est pas très rigoureux :hum:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:48
par Nightmare » 18 Juin 2012, 22:48
Non, mais peut être que ça pourrait nous donner l'idée d'une forme générique des solutions?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 22:51
par Dinozzo13 » 18 Juin 2012, 22:51
Je veux bien mais pour l'instant ...
Les fonctions puissances semblent convenir;
La valeur absolue;
Et ses combinaisons :
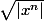
.
Mais comment fais-tu pour trouver toutes ces solutions ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 22:55
par Nightmare » 18 Juin 2012, 22:55
Oui, mais globalement tout ça, ce sont des puissances de x et de la valeur absolue de x. Il faudra juste faire attention avec les puissances non entières aux soucis de domaine de définition.
Bref, maintenant qu'on sait à quoi s'attendre, il faut résoudre. Sauf erreur, il me semble que tu as déjà dû résoudre une équation vraiment similaire : f(x+y)=f(x)+f(y). Si c'est bien le cas, tu pourrais essayer d'en copier le raisonnement.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 23:00
par Dinozzo13 » 18 Juin 2012, 23:00
Exactement !
J'ai essayé d'adopter un raisonnement similaire mais ça bloque un peu, surtout pour
)
.
Parce que si je conjecture
=[f(x)]^n)
, comment vérifier
)
?
Vu que je trouve deux valeurs pour
)
.
Surtout qu'à un moment donné, on aurait
=[f(1)]^n)
, donc si on veut étendre

de

à
,

puis

, ça pose problème.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 23:02
par Nightmare » 18 Juin 2012, 23:02
Tu as déjà trouvé que soit f(1)=0 ou 1. Pour conclure, il te fallait juste observer que pour tout x , f(x)=f(x).f(1)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 23:03
par Dinozzo13 » 18 Juin 2012, 23:03
Je ne te suis pas :triste:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 23:03
par Nightmare » 18 Juin 2012, 23:03
Qu'est-ce que tu ne suis pas? Tu n'es pas d'accord que f(x)=f(x).f(1)?
Si tu l'es, que donne cette égalité pour les différentes valeurs potentielles de f(1)?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 23:07
par Dinozzo13 » 18 Juin 2012, 23:07
Si je suis d'accord.
Si
=0)
alors
=0)
;
Si
=1)
alors
=f(x))
.
Mais quel intérêt ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Juin 2012, 23:11
par Nightmare » 18 Juin 2012, 23:11
Eh bien, tu as clos le cas f(1)=0 non? Tu peux donc continuer à travailler avec f(1)=1. C'est la même chose que ce que tu as fait pour f(0).
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juin 2012, 23:45
par Dinozzo13 » 18 Juin 2012, 23:45
Nightmare a écrit:Eh bien, tu as clos le cas f(1)=0 non? Tu peux donc continuer à travailler avec f(1)=1. C'est la même chose que ce que tu as fait pour f(0).
Ah ben oui, suis-je bête.
Par contre, je rencontra à nouveau un problème.
une fois montré que pour tout n f(x^n)=[f(x)]^n, en l'étendant à Q, puis à R.
Ca ne donne pas les solutions qu'on a trouvé au début.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
