Bonjour, Voici le probème :
Soit dN/dt=r*N*(1-(N/K)), où r est une constante de proportionnalité et k une limite pour la population.
Question : Résolvez cette équation avec N(o)=N indice 0
Est-Normal que j'obtient N(t)-1/e^(R*T) est que toutes les constantes disparaîssent.
Merci beacoup de l'aide
Équation différentielles
12 messages
- Page 1 sur 1
Johnny_p a écrit:Bonjour, Voici le probème :
Soit dN/dt=r*N*(1-(N/K)), où r est une constante de proportionnalité et k une limite pour la population.
Question : Résolvez cette équation avec N(o)=N indice 0
Est-Normal que j'obtient N(t)-1/e^(R*T) est que toutes les constantes disparaîssent.
Merci beacoup de l'aide
Ben, quand on intègre une intégrale simple, normalement on a une constante à définir qui traîne et la précision d'une condition initiale, détermine la constante, ce qui fait que tout est bien défini. Mais, je ne trouve pas ce que tu trouves...
En intégrant :
La constante C restant à déterminer.
Faisons intervenir la condition initiale :
On peut alors remplacer la constante C par sa valeur dans l'équation :
... sauf erreur !
EDIT : Message corrigé suite à l'aimable intervention de LN1 : merci à lui.
Le retour de l'équation masquée
Cette équation a fait couler beaucoup d'encre, c'est le sujet du bac S 2003 (avec un exercice de géométrie dans l'espace, dont la première question, niveau seconde, na pas été traitée par la moitié des candidats). Elle est aussi tombée en 2005, mais avec des valeurs numériques au lieu de paramètres. Je l'attends de pied ferme pour 2007.
Non inscrit a écrit:J'obtient comme équations différentiel ceci :
N(t)=(K*(e^(r*t))/((e^r*t)+k.c)
Je comprend pas pourquoi lorsque je résoud avec N(o)=N indice o que toutes les constantes disparaîssent.
Merci de l'Aide LN1
Ta formule est bonne
si tu y remplaces t par 0 tu obtiens la condition
ce qui donne
puis en remplaçant dans N(t) et en multipliant numérateur et dénominateur par N_0
(Chimerade a fait une petite erreur de signe avant de faire intervenir la valeur initiale)
si maintenant on utilise des chiffres
Que deviendrait l'équation si on dit :
r= 1/5 , k=2000, n(0)=1500 et que l'on suppose qu'on enlève 125 espèces à chaque années.
dn/dt=(1/5)*N*(1-(N/2000))-125
J'apprécie beaucoup votre aide à tous,
merci encore
r= 1/5 , k=2000, n(0)=1500 et que l'on suppose qu'on enlève 125 espèces à chaque années.
dn/dt=(1/5)*N*(1-(N/2000))-125
J'apprécie beaucoup votre aide à tous,
merci encore
Non inscrit a écrit:Est-ce correct d'obtenir ceci:
(arctan(n-1000))/2000=c-(t/4000)
Non ! Si tu différencies cette expression tu verras que tu ne retombes pas sur la même équation différentielle !
Cela dit, tu t'es peut-être trompé sur les parenthèses... Relis bien, compte-tenu des parenthèses que tu as écrites, ton expression est :
J'ai essayé l'intégration moi-même :
Je trouve :
Pour t=0, on obtient bien :
Et en différenciant, on obtient :
Mais je ne suis pas à l'abri d'une erreur (voir ci-dessus !)
J'obtiens bien =-\frac{t}{20}+C)
avec un domaine de validité troublant :
 doit rester dans l' intervalle
doit rester dans l' intervalle  . Troublant car on peut penser que t est un temps variant sur
. Troublant car on peut penser que t est un temps variant sur 
Je ne suis pas d'accord sur la constante : pour t= 0, on a N = 1500 donc
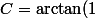 = \pi/4)
Une solution du problème mathématique serait
=-\frac{t}{20}+\pi/4) avec
avec

Mais il s'agit d'un problème pratique donc N ne peut pas être négatif, donc donc
donc  + \pi/4))
Au temps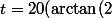 + \pi/4)) , la population s'éteint et la loi ne s'applique plus.
, la population s'éteint et la loi ne s'applique plus.
avec un domaine de validité troublant :
Je ne suis pas d'accord sur la constante : pour t= 0, on a N = 1500 donc
Une solution du problème mathématique serait
Mais il s'agit d'un problème pratique donc N ne peut pas être négatif, donc
Au temps
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
