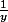Equation differentielle : type bernoulli

[jadrax]

Bonjour voila je doit résoudre

2T²y'(t)-y²(t)=4Ty(t)

Donc dans un premier temps je divise par y² ce qui me donne :



on pose Z=
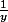
Z'=

j'arrive a -2T²Z'-4TZ=1

et la je bloque...Merci de votre aide

[Ben314]

Bonjour voila je doit résoudre

2T²y'(t)-y²(t)=4Ty(t)

Donc dans un premier temps je divise par y² ce qui me donne :


on pose Z=
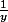
Z'=

j'arrive a -2T²Z'-4TZ=1

et la je bloque...Merci de votre aide

Cela s'appelle une équation différentielle linéaire du premier ordre : tu as surement vu la façon de les résoudre (équation homogène...)

[Ericovitchi]

il ne te manquerais pas un ² sur le Z ? -2T²Z'-4TZ²=1 Et pourquoi = 1 ?
=0 non ?

[jadrax]

oui effectivement il manque un ² sur le Z car il s'agit de -4T*1/y(t)*1/y(t) donc -4TZ²...merci de me l'avoir fait remarquer.

=1 car si je divise le premier menbre par y² on obtient -y²/y²=1 si on fait passer de l'autre coter ca donne 1...non?

donc

Donc au finale cela donne
-2T²Z'-4TZ=1 quand on fait le changement de variable

Bon si cette equation est bonne je vais essayer de voir comment resoudre l'equation differentiellle du premier ordre...par contre j'aurais besoin de cette confirmation car du coup je ne suis plus certain de mon =1....

merci!

[Ben314]

Heuuuuu...
Perso, je trouve bien -2T²Z'-4TZ=1 comme équation "finale".
Par contre, il y a quelques fautes de frappe dans le premier post...

[jadrax]

Oui oui du coup c'est moi qui avait mal écrit une équation ce qui a porter a confusion...j'ai refait mes calculs c'est bien
-2T²Z'-4TZ=1

je vais essayer de résoudre cette équation différentielle et je vous fait part de mon résultat...

[Ericovitchi]

Tu trouves d'abord une solution particulière par exemple une constante
Puis tu l'as résous sans son second membre -2T²Z'-4TZ=0

(en l'écrivant tout simplement Z'/Z=... et en intégrant)

la solution générale est la somme de ta solution particulière + la solution générale de l'équation sans second membre.

[jadrax]

Bon alors je trouve en solution homogene :
Z homogene =

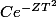
et pour solution particuliere : un polynôme de même degré :
Z=at+B
Z'=a

-2T²a-4T²a-4Tb=1

donc a=6 et b=4

solution particuliere
Z(p)= 6T+4

Au final cela donne :
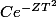
Z(t)=+6T+4
donc Y(t)=

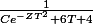
ca vous semble correct?

[Ben314]

Bon alors je trouve en solution homogene :
Z homogene =

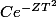
J'ai des doutes...
L'équation (homogène) -2T²Z'-4TZ=0 donne Z'/Z=-2/T donc ta soluce homogène est plûtot Z(t)=C.exp(-(2/T)t)...

Fait gaffe aussi à ne pas confondre la variable de la fonction Z (qui semble être t) et le réel T qui, vu les calculs que l'on fait depuis le début me semble être une constante (sinon, il faut tout reprendre du début...)

[jadrax]

Oui effectivement je retrouve bien comme partie homogène (erreur de calcul...)
Z(t)=Cexp(-(2/T)t)

Pour la solution particulière c'est bien :
Z(p)= 6T+4 ?

ou bien je me suis encore planter dans mes calculs? ce que je n'espère pas!

merci

[Ben314]

...et pour solution particuliere : un polynôme de même degré :

Comme 1 a pour degrés 0, ta solution particulière est de degrés...0, c'est donc une fonction de la forme Z(t)=a et donc Z'(t)=0...

Tu va y arriver...

[jadrax]

donc en prenant Z(p)=a
Z'(p)=0

on remplace ce qui donne :
(-2t²*0)-(4Ta)=1

Donc a=0

donc solution particulière =0?

[Ben314]

Heuuu,
(-2t²*0)-(4Ta)=1 donnerais plutôt a=-1/(4T)...

[jadrax]

J'ai des doutes...
L'équation (homogène) -2T²Z'-4TZ=0 donne Z'/Z=-2/T donc ta soluce homogène est plûtot Z(t)=C.exp(-(2/T)t)...

Fait gaffe aussi à ne pas confondre la variable de la fonction Z (qui semble être t) et le réel T qui, vu les calculs que l'on fait depuis le début me semble être une constante (sinon, il faut tout reprendre du début...)

Ici j'ai juste une question en refaisant mon calcul je tombe sur
Z'/Z=-2/T
ln Z=-2lnT
Z=Ce-2LnT comme solution homogene non?
ici T est la variable

[Ben314]

Depuis le début, la variable de l'équation est T ????
Ton équation de départ est-elle :
I) 2T²y'(t)-y²(t)=4T.y(t) où T est une constante
OU BIEN
II) 2t²y'(t)-y²(t)=4t.y(t) ???

Si on est dans le cas II), tout est à revoir...........

[jadrax]

Oui je suis dsl c'est de ma faute c'est bien le cas 2 ou t est la variable avec y(t)... Du coup normalement la solution homogène est Ce-2lnt si mes calculs sont bon...
Désole encore de vous avoir induit en erreur avec une mauvaise écriture...
Merci

[Ben314]

Bonjour,
Dans ce cas, le début des calculs est le même, mais l'équation homogène Z'/Z=-2/t s'intègre en ln|Z|=-2.ln|t|+cst=ln(1/t²)+cst donc Z=lambda/t^2 où lambda est une constante.
Pour la recherche d'une soluce particulière, je te conseillerais alors la méthode dite "de variation de la constante"...