Équation différentielle de Bernoulli
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 19 Avr 2016, 11:15
par Sarra_sonia » 19 Avr 2016, 11:15
Bonjour,
On considère l' équation de Bernoulli suivante
y^{\frac{1}{2}}+B(x)y)
où

et

sont des fonctions continues sur

.
Si
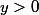
c'est facile, on peut faire le changement de fonction
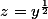
et on obtient l'équation linéaire
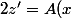+B(x)z)
,
mais si
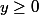
( c'est-à-dire la solution s'annule en un certain

) comment fait-on?
Merci d'avance.
Modifié en dernier par
Sarra_sonia le 20 Avr 2016, 11:32, modifié 1 fois.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 19 Avr 2016, 12:17
par arnaud32 » 19 Avr 2016, 12:17
tu vas devoir dans ce cas recoller des solutions sur les intervalles ou y n'est pas identiquement nulle
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 20 Avr 2016, 11:41
par Sarra_sonia » 20 Avr 2016, 11:41
Je m'excuse, j'ai pas compris comment "recoller des solutions"?
Merci quand même.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Avr 2016, 12:45
par arnaud32 » 20 Avr 2016, 12:45
soit y= 0 partout et c'est bon, soit tu considères
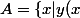>0\})
sur chaque composante connecte de A tu sais trouver une solution.
il te reste a assurer la continuité de y et y' a chaque extrémité de l'intervalle considere
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 24 Avr 2016, 08:54
par Sarra_sonia » 24 Avr 2016, 08:54
merci je vois les choses mieux maintenant.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités