Équation différentielle, solution polynomiale

[Wenneguen]

Bonjour,

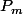
je dois expliciter l'unique solution polynomiale valant 1 en 0 de l'équation différentielle : .

J'essaye de trouver des informations sur son degré, mais je crois que je ne m'y prends pas très bien.

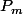
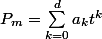
Voici mon raisonnement : soit le degré de . On note Je réécris légèrement l'équation différentielle :
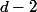
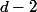
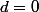
Le premier terme est de degré , tous les autres sont de degré d. Le coefficient du monôme de degré du polynôme est (il provient uniquement de P_m''), et donc en identifiant avec le polynôme nul à droite, j'en déduis ou .

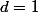
Cela vous semble-t-il correct ? Merci ! :we:

[Black Jack]

En t = 0 : z"(0) + 4m² = 0
z"(0) = -4m²

Soit n le degré de Pm :
z" = a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)

z' = a/(n-1).t^(n-1) + b/(n-2).t^(n-2) + ... - 4m².t + K1

z = a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1

(1-t²).(a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)) - t.(a/(n-1).t^(n-1) + b/(n-2).t^(n-2) + ... - 4m².t + K1) + 4m².(a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1) = 0

(a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)) - (a.t^n + b.t^(n-1) + ... - 4m².t²) - (a/(n-1).t^n + b/(n-2).t^(n-1) + ... - 4m².t² + K1.t) + 4m².(a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1) = 0


coeff en t^n : -a - a/(n-1) + 4m².a/(n(n-1)) = 0
-1 - 1/(n-1) + 4m²/(n(n-1)) = 0

-n(n-1)- n + 4m² = 0

n² - 4m² = 0

n = 2.|m|

Le degré de Pm est 2.|m|
*****
Sauf si je me suis planté... vérifie.

:zen:

[Wenneguen]

En t = 0 : z"(0) + 4m² = 0
z"(0) = -4m²

Soit n le degré de Pm :
z" = a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)

z' = a/(n-1).t^(n-1) + b/(n-2).t^(n-2) + ... - 4m².t + K1

z = a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1

(1-t²).(a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)) - t.(a/(n-1).t^(n-1) + b/(n-2).t^(n-2) + ... - 4m².t + K1) + 4m².(a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1) = 0

(a.t^(n-2) + b.t^(n-3) + ... - 4m².t^(0)) - (a.t^n + b.t^(n-1) + ... - 4m².t²) - (a/(n-1).t^n + b/(n-2).t^(n-1) + ... - 4m².t² + K1.t) + 4m².(a/(n.(n-1)).t^n + b/((n-1)(n-2)).t^(n-1) + ... - 4m².t²/2 + K1.t + 1) = 0


coeff en t^n : -a - a/(n-1) + 4m².a/(n(n-1)) = 0
-1 - 1/(n-1) + 4m²/(n(n-1)) = 0

-n(n-1)- n + 4m² = 0

n² - 4m² = 0

n = 2.|m|

Le degré de Pm est 2.|m|
*****
Sauf si je me suis planté... vérifie.

:zen:

J'ai pas eu le courage de tout relire soigneusement, mais il me semble que ton résultat est correct !
Vois-tu ce qui cloche dans mon raisonnement ? :hein: