Equation dans P(E)!!

[Anonyme]

Bonsoir chers amis
j'ai une question à vous poser s'il vous plait
soit A B C des parties de E
determiner la condition suffisante pour qu'il existe un X dans P(E) tel que AUX=B.
2)résoudre dans P(E) l'equation AUX=B
3) supposons que (c inclu dans A et A inclu dans B)
resoudre dans P(E) le systeme suivant
(AUX=B ;A intersect X=C)

Merci d'avance et bon week end a tous

[phenomene]

Bonjour,

Si tu es un peu perdu, n'hésite pas à faire des dessins (représente chaque ensemble par une "patate"). Ah, les patates... nostalgie de la fameuse époque des mathématiques dites "modernes" ! :ptdr: (Oups, comment être nostalgique d'une époque pendant laquelle on n'était pas encore né).

Bon, pour ton problème, je te laisse vérifier que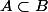 est une condition nécessaire et suffisante pour que l'équation ait une solution. A partir de là, déterminer l'ensemble des solutions n'est pas difficile. Pense à faire intervenir le complémentaire de dans .

Je ne t'en dis pas plus, mais si tu dessines des patates, tout devrait s'éclairer ! :id:

[Anonyme]

oui justement je suis d'acord avec toi phenomenoe . mais comment vous avez fait pour avoir l'idée de faire intervenir le complementaire de A dans B???!!
c une idée géniale! est ce que vous avez d'autres idées pour abordez les problèmes sur les équations ensembliste, car ce genre d'exercie me déstabilise. avez vous un exercice xlassique sur ce genre d'equations?
s'il vous plait je veux tellement maitriser ces equations étrange qui demende un peu d'intuition et un peu de pratique.

merci tout d'aabord pour votre réponse.

[phenomene]

Oh, pour avoir une idée en maths, mon truc, c'est de faire un dessin. En dessinant des patates, le complémentaire de dans se voit tout de suite ! Bon, j'avoue avoir fait le dessin dans ma tête, car j'avais les mains occupées (c'était l'heure de l'apéritif :beer: ), mais ce n'est pas un bon exemple : les maths, ça se fait avec du papier et un crayon. Tiens, ça me rappelle une citation que j'avais mise en exergue d'un devoir donné à mes élèves :
"Nous mathématiciens, on ne coûte pas cher.
Pour travailler, il suffit d'un crayon, de papier et d'un ordinateur.
Ah, j'oubliais, d'une corbeille à papier?
C'est fou ce que l'on peut écrire comme bêtises".
(Jean-Pierre Serre, médaille Fields 1954).

[Anonyme]

Vous avez raison phenomenone.
mais étant donné que je suis encore débutant je n'ai pas encore acquérit ce flair de mathématicien. tant pis pour moi.
j'ai trouvé un exo sur les équation ensembliste /

resoudre dans P(E);
(A intersect X) U (B intersect Xbarre)=enemble vide.
j'aimerais que vous m'aidiez à choisir une piste pour démarrez.
et toujours la meme qustion me tourmente. Quand est je vais posséder le flair
et le pouvoir de résoudre les exercices de la théorie des enembles .
je crois que vous etant prof de math vous pouvez m'éclaircir le chemin.
MERCI BIEN

[phenomene]

.

Bon, les gauchers, dont le cerveau droit (les aires visuelles) est particulièrement développé, dessineront des patates. Pour les droitiers, qui privilégient le cerveau gauche (les aires du langage), on peut essayer de traduire cette équation en langage courant. Etre dans la réunion de deux ensembles, c'est être dans l'un ou l'autre. Dire que la réunion est vide, c'est donc dire que les deux sont vides. A partir de là, ne doit pas rencontrer , et les éléments qui ne sont pas dans ne doivent pas être dans ... Cela donne des informations sur la "localisation" de !

Réponse d'un faux gaucher (peut-être droitier mais ayant décidé de devenir gaucher à cinq ans pour ne pas faire comme les autres) à l'heure du digestif :beer:, à prendre par conséquent avec la méfiance qui s'impose...