EQUATION compliquée

[greg1976]

Bonjour à tous,

je ne parviens pas à calculer la valeur des inconnues X et Y dans le système suivant :

A*(X-Y)/ln[(B-X)/(B-Y)]=C*X=D*Y

où A, B, C et D sont des constantes connues.

Pourvez-vous m'aider?

Merci d'avance.

[sou]

Bonjour à tous,

je ne parviens pas à calculer la valeur des inconnues X et Y dans le système suivant :

A*(X-Y)/ln[(B-X)/(B-Y)]=C*X=D*Y

où A, B, C et D sont des constantes connues.

Pourvez-vous m'aider?

Merci d'avance.

EN fait tu a : (a*(x-y))/[ln(b-x)-ln(b-y)]
ensuite tu passe sous la forme exp pr supprimer les log
>> exp(a*(x-y))/[(b-x)-(b-y)] (n°1)
ensuite si tu veut determiner x tu pose: (n°1)=c*x
ou pr determiner y : (n°1)=d*x
puis une fois que tu as ou x ou y tu va l'utilser pour determiner l autre variable (simple resolution de systeme)

[skilveg]

Bonjour,
D'une part, je ne suis pas convaincu par le fait que (passage au n°1) ni par le fait que passer à l'exponentielle du côté gauche ne change pas le côté droit...

Pour ma part, dans le cas générique (ie par exemple aucun des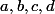 nul) j'injecte 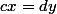dans la première égalité pour éliminer le , et je me retrouve avec
[CENTER]

[/CENTER]
que l'on sait résoudre.

[Black Jack]

condition d'existence : (B-X)/(B-Y) > 0

Si C est différent de 0 --> X = DY/C

A*(X-Y)/ln[(B-X)/(B-Y)] = D*Y devient :

A*(DY/C - Y)/ln[(B- DY/C)/(B-Y)] = D*Y

Si Y est différent de 0 , on divise les 2 membres par Y.

A*(D/C - 1)/ln[(B- DY/C)/(B-Y)] = D

Si D est différent de 0 :

ln[(B- DY/C)/(B-Y)] = (A/D).(D/C - 1)

[(B- DY/C)/(B-Y)] = e^[(A/D).(D/C - 1)]

Et de là, on tire facilement Y = ...
@@@@@@@@

Ensuite, il faut encore traiter les cas où C, D , Y sont conjointement ou non nuls ...


:zen:

[greg1976]

merci à tous