Equas diffs

par **bitonio** » 10 Sep 2006, 16:20

Bonjour à tous,

décidement les équas diff c'est pas mon truc cette semaine :cry:

Je dois résoudre des ED, mais bon ca me pose un problème car elle ne ressemble pas aux formules habituelles

fonction

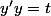
Merci d'avance

(juste un indice ou une formule de départ, pas tout biensur

Au passage, j'en profite pour demander,

pour avoir

, il faut avoir necessairement un a qui est égal à 0 ?

par **Sdec25** » 10 Sep 2006, 16:25

Salut

Pour la première essaie d'intégrer :
la dérivée de u² est 2u'u donc on peut trouver facilement une primitive de u'u :
2u'u=2t donc

, ...

Pour la seconde u'/u²=1 donc

. On cherche ensuite 1/u et finalement u

par **atito** » 10 Sep 2006, 16:26

y'y=t donne que y²=t²+c ( c une constante rèelle)
y'=y² donne que y'=t²+c
donc y est un polynome de degres 3
or y'=y² impossible
alors la solution est l'ensemble vide..

par **bitonio** » 10 Sep 2006, 16:52

bitonio a écrit:Bonjour à tous,

pour avoir , il faut avoir necessairement un a qui est égal à 0 ?

Sinon pour ca, une idée ?

par **atito** » 10 Sep 2006, 16:58

oui il faut absoluement que a soit nul

prend x= 2kPi avec k entier!
Voila

par **bitonio** » 10 Sep 2006, 17:03

donc en fait a est nul et b>1 si j'ai bien pigé ...

par **atito** » 10 Sep 2006, 17:08

exact. Tu utilises la même idée ;-)

par **bitonio** » 10 Sep 2006, 17:12

merci bien :)

au passage (encore une fois), j'en profite pour demander un piste de départ,

si r = a/b est un rationnel, alors cos(ax) + cos(bx) est périodique ... Une idée de départ ?

par **atito** » 10 Sep 2006, 17:23

écrit a/b = p/q ou p et q entier.
Une période est ...... 2pi*p/a!
Salut!

par **bitonio** » 10 Sep 2006, 17:38

hum, peux tu expliciter un tout petit peu plus je n'arrive toujours pas à partir.

Merci d'avance

par **atito** » 10 Sep 2006, 17:40

cos[a(x+2Pi * p/a)] = cos(ax + 2*Pi*p) = cos(ax)
cos[b(x+2Pi * p/a)] = cos(bx + 2*Pi*q) = cos(bx)

Pardon j'ai corrigé la période est 2*pi*p/a

par **bitonio** » 10 Sep 2006, 17:57

J'ai vraiment beaucoup de mal... :triste: Je ne vois pas comment on peut conclure clairement ...

par **atito** » 10 Sep 2006, 18:00

tu sais ce que ca veut dire une fonction périodique?

par **bitonio** » 10 Sep 2006, 18:02

oui biensur cos(ax) = cos(ax + P)

par **atito** » 10 Sep 2006, 18:05

bien sur que non !!!
c'est plutôt cos[a(x+p)]=cos(ax)
l'inconnue est x. relis alors mes postes ça te donnera la solution

par **bitonio** » 10 Sep 2006, 18:07

Ahh mais je suis trop bete moi... forcement que c'est cos(ax) = cos(a(x+p))

Jss désolé la fin du week end est difficile :ptdr: J'ai honte desfois (maintenant par exemple :p)

Merci tout est ok

Bonne soirée

par **atito** » 10 Sep 2006, 18:10

faut jamais avoir honte :p ( en tout cas en posant des questions en maths ..)
C'est un plaisir pour moi ;-) bonne soirée

par **bitonio** » 10 Sep 2006, 18:21

Une idée pour la réciproque :D ?

par **atito** » 10 Sep 2006, 18:26

ya toujours des idées :p
quel réciproque?

par **bitonio** » 10 Sep 2006, 18:33

Montrer que si r=b/a est un nombre rationnel, alors f est périodique (f(x) = cos(ax) + cos(bx)

Démontrer la réciproque (indication, on pourra considérer une combinaison linéaire astucieuse de f et f ''

Equas diffs

Equas diffs

Qui est en ligne