Ensembles de complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 16 Nov 2011, 05:31
par mehdi-128 » 16 Nov 2011, 05:31
Bonsoir, je bloque sur l'exo suivant :
Trouver tous les ensembles de trois complexes (u,v,w) de module 1 tels que :

Merci
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 16 Nov 2011, 09:01
par arnaud32 » 16 Nov 2011, 09:01
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 16 Nov 2011, 23:19
par mehdi-128 » 16 Nov 2011, 23:19
Merci mais je vois pas trop en quoi ça m'avance.
Et la partie :
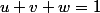
?
-
eloudie06
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Mai 2008, 10:58
-
 par eloudie06 » 17 Nov 2011, 10:18
par eloudie06 » 17 Nov 2011, 10:18
Voilà sur quoi je suis partie, mais je ne suis pas sure que ce soit la bonne méthode à suivre...
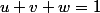

+isin(x)+cos(y)+isin(y)+cos(z)+isin(z)=1)
d'où
+cos(y)+cos(z)=1)
et
+sin(y)+sin(z)=0)
Avec
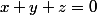
on obtient un système de 3 équations à 3 inconnues...mais bon je ne sais pas comment le résoudre, je sais pas si il faut faire ça, si quelqu'un a une idée?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 17 Nov 2011, 19:04
par mehdi-128 » 17 Nov 2011, 19:04
Il me faudrait résoudre :
+cos(y)+cos(z)=1 \\ sin(x)+sin(y)+sin(z)=0 })
Quelqu'un à une idée ?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 17 Nov 2011, 20:26
par Le_chat » 17 Nov 2011, 20:26
Salut. On a (uv+wv+uw)=1/w+1/u+1/v, et comme u, v et w sont de module 1, le conjugué de u est 1/u, de v, 1/v etc., donc (uv+vw+uw)=1 (qui est le conjugué de w+v+u!)
On considère alors P=(X-u)(X-v)(X-w). En développant, P=X^3-(u+v+w)X^2+(uv+uw+vw)X-uvw
i.e. P=X^3-X^2+X-1, tu dois pouvoir trouver u, v et w grace à ça!
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 17 Nov 2011, 20:31
par mehdi-128 » 17 Nov 2011, 20:31
Le_chat a écrit:Salut. On a (uv+wv+uw)=1/w+1/u+1/v, et comme u, v et w sont de module 1, le conjugué de u est 1/u, de v, 1/v etc., donc (uv+vw+uw)=1 (qui est le conjugué de w+v+u!)
On considère alors P=(X-u)(X-v)(X-w). En développant, P=X^3-(u+v+w)X^2+(uv+uw+vw)X-uvw
i.e. P=X^3-X^2+X-1, tu dois pouvoir trouver u, v et w grace à ça!
Ca me donne :

Ca m'avance pas des masses
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 17 Nov 2011, 20:55
par Le_chat » 17 Nov 2011, 20:55
Sisi! Quelles sont les racines de P?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 18 Nov 2011, 00:11
par mehdi-128 » 18 Nov 2011, 00:11
Le_chat a écrit:Sisi! Quelles sont les racines de P?
u, v et w.
Ca me donne :



Mais après, je vois pas trop.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités