Ensemble de n éléments
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 00:58
par mehdi-128 » 13 Sep 2010, 00:58
Bonsoir, je n'ai aucune idée concernant la résolution de cet exercice :
Soit un ensemble E ayant n éléments
1) On choisit un élément a quelconque dans E. Expliquer pourquoi il y a autant de parties de E qui ne contiennent pas a que de parties de E qui contiennent a.
2) Utiliser la question 1) pour démontrer par récurrence que un ensemble de n éléments possède

parties.
Merci d'avance
-
mathelot
 par mathelot » 13 Sep 2010, 03:38
par mathelot » 13 Sep 2010, 03:38
mehdi-128 a écrit:
Soit un ensemble E ayant n éléments
1) On choisit un élément a quelconque dans E. Expliquer pourquoi il y a autant de parties de E qui ne contiennent pas a que de parties de E qui contiennent a.
Bj,
Pour montrer que deux collections, deux ensembles ont le même nombre d'éléments, on ne les compte pas, on les met en correspondance
bijective
exemplePour montrer qu'il y a autant de stylos que de capuchons,
à chaque stylo on associe son capuchon
Pour la question (1), il s'agit d'associer automatiquement à une partie qui contient

une partie qui ne contient pas

Pour la (2), le résultat de (1) permet de diviser le nombre de parties de E par 2 ... fifty-fifty
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 10:49
par mehdi-128 » 13 Sep 2010, 10:49
mathelot a écrit:Bj,
Pour montrer que deux collections, deux ensembles ont le même nombre d'éléments, on ne les compte pas, on les met en correspondance
bijective
exemplePour montrer qu'il y a autant de stylos que de capuchons,
à chaque stylo on associe son capuchon
Pour la question (1), il s'agit d'associer automatiquement à une partie qui contient

une partie qui ne contient pas

Pour la (2), le résultat de (1) permet de diviser le nombre de parties de E par 2 ... fifty-fifty
Je n'arrive toujours pas à résoudre mon exercice ...
-
taeric
- Membre Naturel
- Messages: 15
- Enregistré le: 07 Nov 2009, 04:59
-
 par taeric » 13 Sep 2010, 11:47
par taeric » 13 Sep 2010, 11:47
1) soit la relation R définie sur E par:
soit A ensemble des parties de E ne contenant pas a.
donc une partie C de A est en relation avec B une partie de E si

il faut montrer que la relation R est bijective
2)prendre un ensemble à 1 élément
puis supposé que la proposition est vraie a l'ordre n
et maintenant à l'ordre n+1 on a un seul élément a qu'on ajoute. Donc il y a

parti ne content pas a +

parti contenant a d'après la question 1 qui donne bien
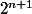
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 12:28
par mehdi-128 » 13 Sep 2010, 12:28
taeric a écrit:1) soit la relation R définie sur E par:
soit A ensemble des parties de E ne contenant pas a.
donc une partie C de A est en relation avec B une partie de E si

il faut montrer que la relation R est bijective
2)prendre un ensemble à 1 élément
puis supposé que la proposition est vraie a l'ordre n
et maintenant à l'ordre n+1 on a un seul élément a qu'on ajoute. Donc il y a

parti ne content pas a +

parti contenant a d'après la question 1 qui donne bien
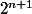
Ah j'ai compris pour la 2. Par contre la 1 je ne sais pas comment montrer que R est bijective ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 13:52
par girdav » 13 Sep 2010, 13:52
Pour la question 1 en notant

la collection des parties de

qui contiennent a et

celles de

qui ne contiennent pas

on définit une application de

dans

qui à

associe

.
On montre que cette application est bijective. La surjectivité n'est pas difficile à voir, l'injectivité non plus, mais on ne sait pas lequel de ces deux points te bloque.
-
mathelot
 par mathelot » 13 Sep 2010, 14:40
par mathelot » 13 Sep 2010, 14:40
Il y avait quelque chose à deviner :hum:
 \rightarrow P(E))
=A^c)

est bijective, envoie les parties contenant

sur les parties ne contenant pas

finalement , la moitié des parties de E (ie, des élements de P(E)) contient

et l'autre moitié ,non
ce qui permet ensuite de récurrer
ça explique pourquoi le cardinal de P(E) est une puissance de 2:
chaque fois que l'on ajoute un élement à E, ça double le nombre de ses sous-ensembles
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 14:53
par mehdi-128 » 13 Sep 2010, 14:53
mathelot a écrit:Il y avait quelque chose à deviner :hum:
 \rightarrow P(E))
=A^c)

est bijective, envoie les parties contenant

sur les parties ne contenant pas

finalement , la moitié des parties de E (ie, des élements de P(E)) contient

et l'autre moitié ,non
ce qui permet ensuite de récurrer
ça explique pourquoi le cardinal de P(E) est une puissance de 2:
chaque fois que l'on ajoute un élement à E, ça double le nombre de ses sous-ensembles
C'est quoi
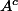
?
Mais je n'arrive pas à comprendre pourquoi

est bijective ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 14:56
par girdav » 13 Sep 2010, 14:56
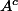
désigne le complémentaire de

dans

. Qu'est-ce qui te pose le plus problème entre l'injectivité et la surjectivité?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 15:06
par mehdi-128 » 13 Sep 2010, 15:06
girdav a écrit: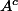
désigne le complémentaire de

dans

. Qu'est-ce qui te pose le plus problème entre l'injectivité et la surjectivité?
On a :
 \rightarrow P(E))
=A^c)
Pour moi

est injective équivaut à :
Pour (x,y) appartenant à A : phi(x)=phi(y) => x=y
Mais je n'arrive pas à l'appliquer ici
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 15:10
par girdav » 13 Sep 2010, 15:10
Il faut montrer que si deux ensembles ont le même complémentaire alors ils sont égaux. Si tu ne connais pas ce résultat je crois qu'il faut le montrer à la main. On peut utiliser le fait que
^c=A)
.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 15:32
par mehdi-128 » 13 Sep 2010, 15:32
girdav a écrit:Il faut montrer que si deux ensembles ont le même complémentaire alors ils sont égaux. Si tu ne connais pas ce résultat je crois qu'il faut le montrer à la main. On peut utiliser le fait que
^c=A)
.
Ah je vois maintenant merci beaucoup. Pour surjective il faut montrer :
Pour tout y appartenant à
)
il existe un x appartenant à A tel que : phi(x)=y
La je bloque
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 15:54
par girdav » 13 Sep 2010, 15:54
Attention,

prend un ensemble et renvoie un autre ensemble. Les éléments n'interviennent pas.
Pour la surjectivité, il faut montrer qu'étant donné

il existe
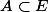
tel que

.
-
mathelot
 par mathelot » 13 Sep 2010, 16:04
par mathelot » 13 Sep 2010, 16:04
mehdi-128 a écrit:Ah je vois maintenant merci beaucoup. Pour surjective il faut montrer :
Pour tout y appartenant à
)
il existe un x appartenant à A tel que : phi(x)=y
La je bloque
Tu n'es pas au bon niveau de logique. On ne raisonne pas sur les éléments de E mais sur les sous-ensembles de E, considérés comme éléments de l'ensemble des parties.
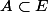
)
A est dans l'ensemble de départ de l'application

exemple

on ne travaille pas sur cet ensemble mais sur P(E) qui a 8 éléments


est une bijection de

sur

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 16:07
par mehdi-128 » 13 Sep 2010, 16:07
girdav a écrit:Attention,

prend un ensemble et renvoie un autre ensemble. Les éléments n'interviennent pas.
Pour la surjectivité, il faut montrer qu'étant donné

il existe
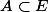
tel que

.
Ah d'accord. Je vois pas d'où partir ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 16:10
par girdav » 13 Sep 2010, 16:10
Il faut encore utiliser le fait que
^c =A)
.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 16:17
par mehdi-128 » 13 Sep 2010, 16:17
mathelot a écrit:Tu n'es pas au bon niveau de logique. On ne raisonne pas sur les éléments de E mais sur les sous-ensembles de E, considérés comme éléments de l'ensemble des parties.
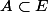
)
A est dans l'ensemble de départ de l'application

exemple

on ne travaille pas sur cet ensemble mais sur P(E) qui a 8 éléments


est une bijection de

sur

Ah je comprend mieux merci beaucoup
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 16:19
par mehdi-128 » 13 Sep 2010, 16:19
girdav a écrit:Il faut encore utiliser le fait que
^c =A)
.
Euh je vois pas comment l'utiliser
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 16:21
par girdav » 13 Sep 2010, 16:21
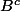
a l'air d'être l'antécédent en question.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Sep 2010, 16:26
par mehdi-128 » 13 Sep 2010, 16:26
girdav a écrit: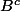
a l'air d'être l'antécédent en question.
Ah j'écris :


On voulait montrer B c E, il existe A c E tel que :

Comme B c E son complémentaire l'est aussi donc on a montré la surjectivité. C'est correct ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
