Encore une serie

[buzard]

Je me rappel avoir fais ca il y a longtemp mais je ne connais plus la reponse. Je pense que la série double suivante est divergente,



mais comment trouve-t-on un equivalent quand ?

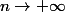
merci pour vos réponses.

[murray]

tu procèdes par encadrement

soit n soit n
alors tu encadres 1/i+j

puis tu sommes les membres de l'inégalité

j'ai trouvé n²/ 2n+2< S(i,j)< n/2

il est ensuite facile de déduire un équivalent

[yos]

Bonjour.
J'ai de gros doutes sur ce que dit murray.
En tout cas moi je trouve comme équivalent.
On peut exprimer en fonction de et ensuite appliquer Cesaro.

[aviateurpilot]

on pose

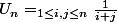
=> soit de N
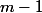
il y a solutions de l'equation x+y=m dans l'intervalle
=> et pour
il y a solutions de l'equation x+y=m dans l'intervalle donc il y a le meme nombre de solutions que le symetrique par rapport a
par exemple , 2n et 2;2n-1 et 3 ; n et n+2.....n+1 et le symetrique de lui meme

donc

[yos]

Rectificatif : comme équivalent de u_n.

[yos]

J'ai pas lu ton truc aviateur mais la divergence est évidente par comparaison à la série harmonique. La recherche d'un équivalent est un peu plus intéressant.

[aviateurpilot]

ah oui,
j'ai vu ma faute
j'ai modifié mais j'ai pas encor trouvé la limite :++:

[buzard]

En tout cas moi je trouve comme équivalent.
On peut exprimer en fonction de et ensuite appliquer Cesaro.

J'arrive à 2n ln 2, car la suite tend bien vers +oo. Merci

pour ceux que ça interresse :



comme à droite c'est divergent, les sommes partielles sont equivalente d'ou le résultat.

PS: cesaro c'est les théorèmes de comparaison de série?

[yos]

Ici Cesaro, c'est pareil que le théorème que tu appliques pour les séries divergentes.
Th. de Cesaro : si tend vers L, alors tend vers L.
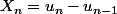
Tu appliques ce théorème avec et tu trouves ton équivalent.