Hop ! Et encore une série...

[HAL 9000]

Voilà encore un p'tit soucis de série...
Sachant que la suite est positive et tend vers l'infini, il me faut montrer que pour :

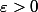
où Q > 0.
Comment le montrer ?

[fahr451]

la somme c'est bien

sigma sur k = 1 à l des ak al ?

[fahr451]

on pose

vl = al sigma k = 1 , ..., l ak

on a vl ->+infini
on pose x = Q/epsilon^^2 on a x->+infini
on pose f(x) = max (l , vl =< x )

il est clair que le max existe car vl ->+infini

il est clair que f croit car si 0
et l tel que vl =< x alors a fortiori vl =< x'
f a donc une limite L en +infini

or on a vl =< vl ce qui prouve que f ( vl) >= l

et par passage à la limite L = +infini

[HAL 9000]

merci... mais en fait le paramètre est epsilon, donc si epsilon1 < epsilon2 alors le max sur les l est une fonction décroissante plutot non (0 < epsilon < 1) ?
De plus j'ai du mal a comprendre ton raisonnement.... Il faut que je montre que lorsque epsilon tend vers 0 alors le max pris sur les l tend vers l'infini.

[fahr451]

j ai pris comme paramètre x = Q / epsilon ^2 j ai trouvé plus agréable

car c'est vraiment lui qui compte le Q et le epsilon carré sont trompeurs.

et qd epsilon ->0 x ->+infini

f croit comme fonction de x et décroit donc comme fct de epsilon

[HAL 9000]

Ok, mais après j'ai du mal a comprendre... peux tu m'expliquer ?

[fahr451]

la croissance c 'est ok ?
donc L est la limite de f en + infini

je vais prendre une suite de x qui tend vers +infini bien choisi e


x = vn on a bien vn=< vn = x donc n est dans l'ensemble des l tels que vl =< x donc le max de cet ensemble d 'indices est supérieur à n

ce max s 'appelle par définition f ( v n )


d'où f ( v n ) >= n


ensuite je passe à la limite ds l inégalité lim f (v n ) = + infini

or puisque v n ->+infini et f - > L en +infi par composition des limites

f ( v n ) - > L

ce qui prouve L = +infini

[HAL 9000]

Ok pour lapremiere partie. Par contre je dirai que f(vn) = n puisque tu pose vn = x donc n est le max tel que vn <= x non ? et ca ne change pas du coup le résultat.

[fahr451]

et tu aurais tort de dire f(v n ) = n

car rie n n 'empèche que v (n+1) =< v n

la suite v n n 'est pas forcément croissante ...

[HAL 9000]

c juste... merci pour tes réponses :++:.