La voici, tin tin...
" Si f:Rn->R continue est nulle presque partout, alors f=0 (la fonction identiquement nulle)"
Ca veut dire quoi?? Que si f=0 presque partout alors automatiquement f=0??
On ne peut pas avoir simplement "f=0 presque partout" ?
(En fait la preuve s'appuit sur le fait que si f n'est pas nulle, alors en une boule centrée en un point de Rn f n'est pas nulle. Et comme la mesure de cette boule n'est pas nulle alors f n'est pas nulle presque partout.
Mais pourquoi n'aurait ton pas une boule de mesure nulle?? de rayon 1/n par exemple quand n tend vers l'infini??
Enfin bref, si on pouvait m'éclairer svp...
mercii
Encore une petite question
18 messages
- Page 1 sur 1
par abcd22 » 24 Avr 2006, 20:43
Bonjour !
La boule qu'on trouve au voisinage d'un point où f n'est pas nulle n'est pas de mesure nulle car avec la définition de la continuité on trouve une boule d'un rayon strictement positif donné (qu'on fixe pour la suite de la démo) sur laquelle f est strictement positive ou négative, et on intègre f sur cette boule pour prouver que f est nulle.
La boule qu'on trouve au voisinage d'un point où f n'est pas nulle n'est pas de mesure nulle car avec la définition de la continuité on trouve une boule d'un rayon strictement positif donné (qu'on fixe pour la suite de la démo) sur laquelle f est strictement positive ou négative, et on intègre f sur cette boule pour prouver que f est nulle.
par simplet » 25 Avr 2006, 07:38
ce que je voudrais qu'on m'affirme c'est qu'une fonction nulle presque partout et continue, ne peut pas "rester simplement" nulle presque partout.
Mais si on prend une fonction nulle, qui a un certain endroit fait un petit triangle de base 2/n... quand n tend vers 0 cette fonction est toujours continue...et tend vers la fonction nulle... mouais.. c'est pas vraiment un contre exemple ca..
je sais pas, si qqun a quelque chose a rajouter...
Mais si on prend une fonction nulle, qui a un certain endroit fait un petit triangle de base 2/n... quand n tend vers 0 cette fonction est toujours continue...et tend vers la fonction nulle... mouais.. c'est pas vraiment un contre exemple ca..
je sais pas, si qqun a quelque chose a rajouter...
par Touriste » 25 Avr 2006, 08:31
Bonjour,
Effectivement, une fonction continue nulle presque partout est nulle partout. Comme cela a été dit, s'il existe un point où ta fonction n'est pas nulle, on pourra trouver une petite boule ouverte autour de ce point telle que la fonction appliquée en n'importe quel point de cette boule soit non nulle, ce qui contredit le fait que la fonction soit nulle p.p. Pour mémoire, le seul ouvert de mesure nulle de R^n est l'ensemble vide.
Si on retire l'hypothèse de continuité, le résultat est bien sûr faux. Il suffit de prendre l'indicatrice de Q pour s'en convaincre (fct nulle p.p. mais pas partout).
Effectivement, une fonction continue nulle presque partout est nulle partout. Comme cela a été dit, s'il existe un point où ta fonction n'est pas nulle, on pourra trouver une petite boule ouverte autour de ce point telle que la fonction appliquée en n'importe quel point de cette boule soit non nulle, ce qui contredit le fait que la fonction soit nulle p.p. Pour mémoire, le seul ouvert de mesure nulle de R^n est l'ensemble vide.
Si on retire l'hypothèse de continuité, le résultat est bien sûr faux. Il suffit de prendre l'indicatrice de Q pour s'en convaincre (fct nulle p.p. mais pas partout).
par Zebulon » 25 Avr 2006, 08:44
Bonjour,
je ne comprends pas. Ne prouve-t-on pas au contraire que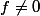
? Puisqu'en intégrant la fonction sur la boule, on va trouver une valeur strictement positive ou stritement négative. On dit que }dt}]\le\int_{boule\ ouverte}[{f(t)}]dt)
donc ???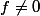
J'ai mis entre crochets les valeurs absolues.
Si l'on pouvait m'expliquer ce serait sympa. Au passage, si on pouvait me dire comment mettre des valeurs absolues...
Merci d'avance.
je ne comprends pas. Ne prouve-t-on pas au contraire que
J'ai mis entre crochets les valeurs absolues.
Si l'on pouvait m'expliquer ce serait sympa. Au passage, si on pouvait me dire comment mettre des valeurs absolues...
Merci d'avance.
par Touriste » 25 Avr 2006, 08:48
Salut,
On fait un raisonnement par l'absurde : on suppose qu'il existe un point où f est non nulle et on montre qu'elle ne peut pas être nulle p.p.
Pour les valeurs absolues, utilise la barre verticale qui doit figurer sur une touche de ton clavier (combinaison avec AltGr). Il n'y a pas de commande particulière.
On fait un raisonnement par l'absurde : on suppose qu'il existe un point où f est non nulle et on montre qu'elle ne peut pas être nulle p.p.
Pour les valeurs absolues, utilise la barre verticale qui doit figurer sur une touche de ton clavier (combinaison avec AltGr). Il n'y a pas de commande particulière.
par Zebulon » 25 Avr 2006, 08:53
La question n'était-elle pas de montrer que:
Pour les valeurs absolues, j'ai beau chercher, je ne trouve pas de barre verticale sur mon clavier...
simplet a écrit:"Si f:Rn->R continue est nulle presque partout, alors f=0 (la fonction identiquement nulle)"
Pour les valeurs absolues, j'ai beau chercher, je ne trouve pas de barre verticale sur mon clavier...
par serge75 » 25 Avr 2006, 08:55
Simplet, j'ai comme l'impression que tu fais une erreur de raisonnement.
Ton n de R^n est fixé !
Bref, par l'absurde, si f continue n'est pas nulle partout ; soit x un point où f(x) est non nul.
On prend alors epsilon=(1/2)(la norme de f(x)). Tu remarqueras que epsilon est fixé !
de la continuité en x, il existe alors une boule de rayon alpha fixé (centrée en x) sur laquelle f(t) est non nul (écrire que la distance de f(t) à f(x) est
Ton n de R^n est fixé !
Bref, par l'absurde, si f continue n'est pas nulle partout ; soit x un point où f(x) est non nul.
On prend alors epsilon=(1/2)(la norme de f(x)). Tu remarqueras que epsilon est fixé !
de la continuité en x, il existe alors une boule de rayon alpha fixé (centrée en x) sur laquelle f(t) est non nul (écrire que la distance de f(t) à f(x) est
par serge75 » 25 Avr 2006, 09:00
Pour la non nullité de la mesure de la boule de rayon alpha>0.
Par équivalence des normes en dimension finie, cette boule contient une boule-infinie (ie : boule pour la norme infinie, ou en d'autres termes un pavé) de rayon r>0. Pour la mesure de Lebesgues, ce pavé est de mesure r^n. Donc la mesure de la boule est >= à r^n. cqfd.
Par équivalence des normes en dimension finie, cette boule contient une boule-infinie (ie : boule pour la norme infinie, ou en d'autres termes un pavé) de rayon r>0. Pour la mesure de Lebesgues, ce pavé est de mesure r^n. Donc la mesure de la boule est >= à r^n. cqfd.
par Zebulon » 25 Avr 2006, 09:01
f nulle presque partout, celà veut-il dire f nulle partout sauf en un nombre fini de point?
Serge ou Touriste, ma réponse était-elle correcte?:
Serge ou Touriste, ma réponse était-elle correcte?:
Zebulon a écrit:donc
par Touriste » 25 Avr 2006, 09:03
Zebulon a écrit:f nulle presque partout, celà veut-il dire f nulle partout suaf en un nombre fini de point?
Non. L'indicatrice de Q est nulle p.p. mais Q n'est pas fini... "nulle p.p." signifie "nulle en dehors d'un ensemble de mesure de Lebesgue nulle".
par serge75 » 25 Avr 2006, 09:04
Zebulon, nulle sauf en un nombre fini de point (et même sauf en un nombre dénombrable de points) est un cas particulier de nulle presque partout.
Nulle presque partout veux dire nulle sauf sur un ensemble de mesure nulle. Si tu ne connais pas encore la théorie de la mesure (niveau licence), il me sera dur de t'en dire plus.
Nulle presque partout veux dire nulle sauf sur un ensemble de mesure nulle. Si tu ne connais pas encore la théorie de la mesure (niveau licence), il me sera dur de t'en dire plus.
par Zebulon » 25 Avr 2006, 09:06
En fait, j'étais en licence cette année, mais j'ai arrêté en Janvier. Je ne connais donc pas la théorie de la mesure. Je regarderai dans un bouquin.
Merci quand même de m'avoir répondu.
Merci quand même de m'avoir répondu.
par serge75 » 25 Avr 2006, 09:39
Les principales étapes de la construction de la mesure de Lebesgue sur R :
On appelle tribu sur un ensemble X (X=R ici) toute partie T de l'ensemble P(X) des parties de X qui soit stable par réunion dénombrable, stable par passage au complémentaire, et contenant X. Les parties de A qui sont dans T sont alors dites mesurables.
Si S est une partie de P(X), l'intersection des tribus contenant S est une tribu appelée tribu engendrée par S. C'est la plus petite tribu contenant S.
La tribu engendrée par les ouverts (de R) s'appelle la tribu borélienne de R, et ses éléments sont les boréliens.
On définit la mesure (ou la longueur) d'un intervalle ouvert ]a,b[ avec aOn étend ensuite la mesure à tous les boréliens suivant un procédé que je n'expliciterai pas, et qui vérifie en particulier :
Si A et B sont mesurables et disjoints, alors m(A union B)=m(A)+m(B); si (An) est une suite croissante de boréliens, alors la mesure de leur réunion est la limite des mesures des An ; si A et B sont deux boréliens tels que A inculs dans B, alors m(a)<=m(B).
On remarquera au passage que m est à valeurs dans [0,+infini] (infini peut être atteint : la mesure de R est l'infini).
Enfin, ultime étape : on appelle négligeable tout ensemble (borélien ou pas) inclus dans un ensemble de mesure nulle. Un négligeable borelien est nécessairement de mesure nulle.
La tribu de Lebesgue est l'ensemble des ensembles du type (A union B) où A est borélien et B négligeable. La mesure d'un tel ensemble est alors par définition la mesure de A (dont on montre qu'elle ne dépend pas d'une telle décomposition).
Enfin, tout ensemble dénombrable est mesurable au sens de Lebesgues, et de mesure nulle. Voili voilà.
On appelle tribu sur un ensemble X (X=R ici) toute partie T de l'ensemble P(X) des parties de X qui soit stable par réunion dénombrable, stable par passage au complémentaire, et contenant X. Les parties de A qui sont dans T sont alors dites mesurables.
Si S est une partie de P(X), l'intersection des tribus contenant S est une tribu appelée tribu engendrée par S. C'est la plus petite tribu contenant S.
La tribu engendrée par les ouverts (de R) s'appelle la tribu borélienne de R, et ses éléments sont les boréliens.
On définit la mesure (ou la longueur) d'un intervalle ouvert ]a,b[ avec aOn étend ensuite la mesure à tous les boréliens suivant un procédé que je n'expliciterai pas, et qui vérifie en particulier :
Si A et B sont mesurables et disjoints, alors m(A union B)=m(A)+m(B); si (An) est une suite croissante de boréliens, alors la mesure de leur réunion est la limite des mesures des An ; si A et B sont deux boréliens tels que A inculs dans B, alors m(a)<=m(B).
On remarquera au passage que m est à valeurs dans [0,+infini] (infini peut être atteint : la mesure de R est l'infini).
Enfin, ultime étape : on appelle négligeable tout ensemble (borélien ou pas) inclus dans un ensemble de mesure nulle. Un négligeable borelien est nécessairement de mesure nulle.
La tribu de Lebesgue est l'ensemble des ensembles du type (A union B) où A est borélien et B négligeable. La mesure d'un tel ensemble est alors par définition la mesure de A (dont on montre qu'elle ne dépend pas d'une telle décomposition).
Enfin, tout ensemble dénombrable est mesurable au sens de Lebesgues, et de mesure nulle. Voili voilà.
par Zebulon » 25 Avr 2006, 09:53
Merci beacoup pour cette explication.
Petit lapsus...? :ptdr:
Juste je ne comprends pas ce qu'est une suite croissante de boréliens. S'agit-il de boréliens inclus les uns dans les autres?
serge75 a écrit:inculs
Petit lapsus...? :ptdr:
Juste je ne comprends pas ce qu'est une suite croissante de boréliens. S'agit-il de boréliens inclus les uns dans les autres?
par serge75 » 25 Avr 2006, 11:18
Oui : suite croissante pour l'inclusion ; en d'autres termes, pour tout n, A_n est inclus dans A_(n+1).
Quand au lapsus.... euh ! :we:
Quand au lapsus.... euh ! :we:
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :