Enchaînement difficile
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 19 Déc 2010, 19:42
Bonsoir
Voici un exercice sur lequel je me casse les dents depuis quelque temps. Aurez-vous meilleur appétit que moi ?
On cherche la limite pour
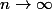
de
sans utiliser Stirling.
Pour cela, on pose
et
1) Montrer que
on a
)
... facile ...
2) En déduire
)
puis
pour
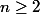
... toujours facile ...
3) Montrer que pour
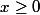
on a
\le x)
Jusque là, tout va bien ...
4) En déduire que
pour
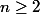
Alors là !!!
Je ne vois pas en particulier comment le
peut correspondre au
. Ce qui est sûr, c'est que l'encadrement est correct.
Si quelqu'un a une idée, elle sera bienvenue.
-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
par fatal_error » 19 Déc 2010, 21:38
salut,
alors jfais dans la dentèle :
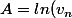 = nln(n) - \bigsum_{k=1}^n ln(k))
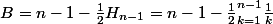
et le but c'est de montrer A>B
soit
? :
 \ge n-1 - \frac{1}{2} \bigsum_{k=1}^{n-1} \frac{1}{k} + \bigsum_{k=1}^{n-1}ln(k) + ln(n))
? :
 - ln(n) + 1 -n \ge -\frac{1}{2} \bigsum_{k=1}^{n-1} \frac{1}{k} + \bigsum_{k=1}^{n-1}ln(k))
? :
(ln(n) -1) \ge \bigsum_{k=1}^{n-1} [ ln(k)-\frac{1}{2k} ])
là, on a n-1 termes a gauches comme a droite, pis comme
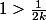
et ln(n) supérieur à ln(k), ca doit etre good
edit ben merde chais même plus soustraire :marteau:
la vie est une fête
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 19 Déc 2010, 22:36
C'est pas évident évident
Et pourquoi avoir posé la question 3 ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 19 Déc 2010, 23:23
Bonjour,
je crois qu'il faut s'aider de
)
.
-
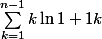fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
par fatal_error » 20 Déc 2010, 12:13
me revoilà!
alors cte fois jtente ca :
avec
et
On a par hypothèse de récurrence
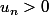
Now, on veut montrer que
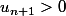
alors
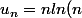 - \bigsum_{k=1}^nln(k)-n+1+\frac{1}{2}H_{n-1})
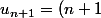ln(n+1) - \bigsum_{k=1}^{n+1}ln(k) -n+1 -1 + \frac{1}{2}H_n)
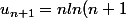 + ln(n+1) - \bigsum_{k=1}^{n}ln(k) - ln(n+1) -n+1 -1 + \frac{1}{2}H_{n-1} + \frac{1}{2n})
On bidouille le
)
:
 = n[ ln(n(1+\frac{1}{n}))]=n(ln(n) + ln(1+\frac{1}{n})))
On remplace dans
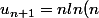 -\bigsum_{k=1}^nln(k) -n+1 + \frac{1}{2}H_{n-1} + nln(1+\frac{1}{n}) -1 +\frac{1}{2n})
La soustraction
nous donne
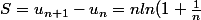 -1 + \frac{1}{2n})
pis là on utilise ton inégalité...
 - 1 +\frac{1}{2n}\\<br />S \ge 1 - \frac{1}{2n} -1 + \frac{1}{2n}\\<br />S \ge 0)
Donc
_{n\in \mathbb{n}})
est croissante pour
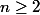
, et comme avec un peu de chance
, alors
est positive pour tout n...sinon c'est BALLO XD
la vie est une fête
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 20 Déc 2010, 12:35
On a :
&=\sum_{k=1}^{n-1}k\ln(k+1)-\sum_{j=1}^{n-1}j\ln j\\<br />&= \sum_{j=2}^n(j-1)\ln j-\sum_{j=2}^{n-1}j\ln j\\<br />&= (n-1)\ln n-\sum_{j=2}^{n-1}\ln j\\<br />&= \ln\(\fr{n^{n-1}}{(n-1)!}\)\\<br />&=\ln \(\fr{n^n}{n!}\)<br />\end{align})
.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 20 Déc 2010, 16:14
Bien vu Girdav.
Toutes mes félicitations ...
Merci aussi Fatal error.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 20 Déc 2010, 16:43
En fait j'ai un peu "triché" pour le trouver. J'ai commencé par écrire que
\leq \sum_{k=1}^{n-1}k\ln\(1+\fr 1k\))
.
Mais il est vrai que ç'aurait été (beaucoup) plus simple avec une question 3.bis : montrer que
)
.
-
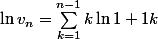Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 20 Déc 2010, 17:10
Salut,
A la limite (je dit bien à la limite), cette astuce peut sembler naturelle si on se dit qu'on va essayer de faire le 4) par récurence car cela signifie que l'on va étudier ln(v(n+1))-ln(vn) qui n'est autre que ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
