égalité délicate
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 22 Oct 2006, 17:03
par BiZi » 22 Oct 2006, 17:03
bonjour,
je sèche sur l'égalité suivante à montrer:
p= produit (1-r^j) , j allant de 1 à p-1
et r= exp(2pi*i/p), i est bien sur le complexe tel que i²=-1
j'ai pensé à factoriser r^j-1 mais cela ne donne rien
Merci de me débloquer!
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 22 Oct 2006, 17:46
par abcd22 » 22 Oct 2006, 17:46
Bonjour,
On peut utiliser le polynôme
 = \frac{\prod_{i=0}^{p-1} (X - r^j)}{X-1})
, on le simplifie en remarquant que les r^j pour j = 0...p-1 sont les racines pièmes de l'unité et on calcule P(1).
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 22 Oct 2006, 18:38
par BiZi » 22 Oct 2006, 18:38
merci pour ta réponse
Néanmoins, je n'arrive pas à simplifier le polynôme P.
comment utilises-tu le fait que les r^j soient les racines n ièmes de l'unité ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Oct 2006, 18:40
par tize » 22 Oct 2006, 18:40
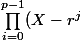= X^p-1)
non ?
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 22 Oct 2006, 18:44
par BiZi » 22 Oct 2006, 18:44
comment parviens-tu à cette égalité ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Oct 2006, 18:46
par tize » 22 Oct 2006, 18:46
ba qu'est ce qui annule le polynome du membre de gauche?
Qu'est ce qui annule celui du membre de droite ?
egalité avec coef dominant ...
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 22 Oct 2006, 19:53
par BiZi » 22 Oct 2006, 19:53
tize a écrit: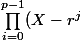= X^p-1)
non ?
en fait, j'avais oublié quelque chose de fondamental dans mon énoncé initial:p est premier. l'égalité ci dessus n'est pas vrai si on oublie cette hypothèse.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Oct 2006, 20:22
par yos » 22 Oct 2006, 20:22
BiZi a écrit:en fait, j'avais oublié quelque chose de fondamental dans mon énoncé initial:p est premier. l'égalité ci dessus n'est pas vrai si on oublie cette hypothèse.
Mais si mais si !
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 22 Oct 2006, 20:50
par BiZi » 22 Oct 2006, 20:50
exact; mea culpa.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
