Dualité et trialité

[barbu23]

Bonjour à tous,

J'aimerais pouvoir décomposer l'espace des matrices carrées d'ordre en la somme directe de trois autres espaces particuliers que j'aimerais détérminer leur caractéristiques :

On pose :

de façon à avoir :
et

Donc, mon but est de détérminer : , et de la manière suivante :
Et :

Question :

Par quoi peut - t - on remplacer et , en fonction de , pour que la somme soit directe ?

Je cherche à suivre la même démarche, que celle empruntée, pour établir que : .
Je cherche et les plus naturellement possibles.
Comme c'est le cas de :

: l'ensemble des matrices carrés d'ordre
: l'ensemble des matrices carrés, antisymétriques, d'ordre
: l'ensemble des matrices carrés, symétriques, d'ordre

, parce que :

Merci d'avance. :happy3:

[barbu23]

On m'a dit que, la matrice transposée qui apparaît dans le cas de la décomposition : est directement liée à la notion d'application linéaire duale . Il faut donc, voir comment définir la trialité : contrairement à la dualité, il n'y a pas un seul espace vecteur trial mais deux (un qui correspond à et l'autre à ). À partir de là, se définissent naturellement la première et la seconde application linéaire triales d'un endomorphisme donné et sur les matrices associées.

Rappel :

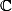
Soit un - espace vectoriel de dimesnion , muni de sa base canonique :.
Soit le dual de , muni de sa base duale :
Par définition, la transposée d'un endomorphisme ayant pour matrice correspondante : , est l'application telle que : . Cela permet de définir la matrice transposée qui est la matrice correspondante de l'endomorphisme transposé : .
est l'unique endomorphisme de , qui verifie : , pour tous .

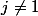
Je n'arrive pas à comprendre cette notion de trialité, ni, imaginer comment ils sont construits, les deux espaces trials de . Quelles sont les caractéristiques de ces deux espaces, et quel est leur lien avec et tel que et ?

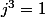
[barbu23]

Voici comment je conçois les choses :

L'idée qui nous a poussé à définir à partir d'un espace vectoriel son dual et don biduale , c'est la cyclicité de tel que : ( i.e : ), Bref, vérifie l'équation dans l'espace des espaces vectoriels.

J'aimerais pouvoir appliquer le même principe pour la trialité, qui définit une - cyclicité et qui permet de definir l'espace tridual tel que ( ce qui correspond à la résolution de l'equation dans l'espace des espaces vectoriels )

Quelle piste à suivre ?.
Comment se construit le dual de quant ?

Merci d'avance. :happy3:

[barbu23]

Voici comment je conçois les choses :

L'idée qui nous a poussé à définir à partir d'un espace vectoriel son dual et don biduale , c'est la cyclicité de tel que : ( i.e : ), Bref, vérifie l'équation dans l'espace des espaces vectoriels.

J'aimerais pouvoir appliquer le même principe pour la trialité, qui définit une - cyclicité et qui permet de definir l'espace tridual tel que ( ce qui correspond à la résolution de l'equation dans l'espace des espaces vectoriels )

Quelle piste à suivre ?.
Comment se construit le dual de quant ?

Merci d'avance. :happy3:

[DamX]

Voici comment je conçois les choses :

L'idée qui nous a poussé à définir à partir d'un espace vectoriel son dual et don biduale , c'est la cyclicité de tel que : ( i.e : ), Bref, vérifie l'équation dans l'espace des espaces vectoriels.

J'aimerais pouvoir appliquer le même principe pour la trialité, qui définit une - cyclicité et qui permet de definir l'espace tridual tel que ( ce qui correspond à la résolution de l'equation dans l'espace des espaces vectoriels )

Quelle piste à suivre ?.
Comment se construit le dual de quant ?

Merci d'avance. :happy3:

Hello,

Je n'ai pas tout suivi mais si je ne dis pas de bêtises en dimension finie tu as toujours "E** = E". (je mets des crochets parce qu'ils sont identifiables même si ce n'est pas le même objet). Du coup je ne vois pas trop ce que tu essayes de faire, tu n'auras jamais ta "3-cyclicité", à moins (et là je spécule totalement) de donner carrément une définition différente à "E*" mais ce ne sera plus le "dual" au sens propre.

[barbu23]

Hello,

Je n'ai pas tout suivi mais si je ne dis pas de bêtises en dimension finie tu as toujours "E** = E". (je mets des crochets parce qu'ils sont identifiables même si ce n'est pas le même objet). Du coup je ne vois pas trop ce que tu essayes de faire, tu n'auras jamais ta "3-cyclicité", à moins (et là je spécule totalement) de donner carrément une définition différente à "E*" mais ce ne sera plus le "dual" au sens propre.

Bonjour Dam'X :
Merci pour ces précisions.
Oui, j’accepte de changer la définition de , pour avoir .
Comment devient dans ce cas ? et, est ce qu'il existe une application canonique ( Un isomorphisme, de préférence ) entre et qui permet de mettre en lien la base de et la base de , comme c'est le cas où quant il s'agit du dual de : dans le cas habituel ?
Merci d'avance.

[barbu23]

Voici ce que j'ai eu comme réponse sur un autre forum :

Bonsoir,

Je crois comprendre que Pablo s'intéresse au problème suivant : il observe que la transposition de matrices vue comme endomorphisme de admet pour polynôme minimal . La décomposition en somme directe matrices symétriques + matrices antisymétriques peut alors se voir comme application du lemme des noyaux (ou beaucoup plus directement bien sûr). Maintenant Pablo cherche à savoir si on peut trouver une décomposition naturelle du même genre mais avec trois sous-espaces.

Une idée simple est de considérer un endomorphisme de dont le polynôme soit annulateur, ce qui donnera une décomposition de en somme directe :

À quoi ressemblent les projecteurs associés à cette décomposition ? Dans le cas de la transposition, il s'exprimaient de façon remarquablement simple. Si est la décomposition d'une matrice $M$ correspondant à la somme directe ci-dessus, alors et . On en déduit que
, et enfin . C'est bien de la forme recherchée par Pablo.

Maintenant, la question est de trouver un choix naturel de . Dans le cas de on avait la transposition qui apparaissait naturellement via la dualité, c'est pourquoi je proposais de s'intéresser à la trialité pour le cas . Malheureusement je ne connais pas de notion de trialité et je ne sais pas du tout s'il en existe, c'était au choix une piste de réflexion pour Pablo ou une boutade (H s'en est rendu compte). Sauf à trouver un bon $\Phi$, je ne vois pas trop l'intérêt de tout ça.