DSE et continuité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 04 Aoû 2018, 19:48
par Pseuda » 04 Aoû 2018, 19:48
Bonsoir,
Concours E3A PC 2016, il est écrit : montrer que la fonction définie par :
=\dfrac{z(e^{2iz}+1)}{e^{2iz}-1}, T(0)=0)
admet un développement en série entière sur un disque de centre 0 et de rayon > 0.
Il me semble qu'il y a une erreur. Merci d'avance !
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 04 Aoû 2018, 19:53
par FLBP » 04 Aoû 2018, 19:53
Ton erreur vient du fait de la division par 0 quand z vaut 0 ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Aoû 2018, 22:31
par Ben314 » 04 Aoû 2018, 22:31
Salut,
Non, il n'y a pas la moindre erreur : la fonction

est évidement développable en série entière au voisinage de 0 et son développement commence par

(i.e. pas de terme constant).
Donc la fonction

pour

et

est développable en série entière
avec un terme constant non nul donc son inverse

pour

et

est aussi développable en série entière au voisinage de 0 (et si on connaît la théorie des fonctions holomorphes, on peut aussi affirmer sans calculs que le rayon de convergence est R=1 vu qu'elle admet des pôles en
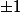
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 04 Aoû 2018, 22:53
par Pseuda » 04 Aoû 2018, 22:53
Bonsoir,
Ok. Le seul souci, c'est que si la fonction T est DSE, donc égale à une série entière, par théorème celle-ci est continue sur le disque de convergence. Or T n'est pas continue en 0 puisque sa limite en 0 est -i. D'où une contradiction.
Modifié en dernier par
Pseuda le 05 Aoû 2018, 07:34, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Aoû 2018, 01:01
par Ben314 » 05 Aoû 2018, 01:01
Ah, effectivement, j'avais même pas regardé que la valeur en 0 était donnée et fausse.
Mais c'est quand même on ne peut plus bénin comme erreur, non ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 05 Aoû 2018, 07:32
par Pseuda » 05 Aoû 2018, 07:32
Bonjour,
Merci. C'est bénin sauf que c'est dans un sujet de concours, et certains élèves peuvent se mettre à recommencer 10 fois le calcul (ce que j'ai fait), ne voulant pas croire à une telle erreur, leur faisant perdre du temps injustement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités