Bonjour à tous,
voilà je comprends bien ce qu'est la droite projective réelle (on projette IR carré sur le cercle unité puis on identifie les points opposés, donc je peux "éliminer" un demi-cercle (fermé d'un coté, ouvert de l'autre) et recoller les deux bords du demi-cercle restant, ce qui fait un cercle).
Je comprends aussi bien ce qu'est le cercle unité avec les projections stéréographiques (on imagine donc qu'on tord la droite réelle et qu'on colle moins l'infini avec plus l'infini, ce qui devient le pôle nord).
Donc on a un cercle des deux cotés... cool ! j'aimerais trouver maintenant trouver une bijection bicontinue entre les deux espace (S1 et droite projective réelle = P1(R)).
Est-ce aussi simple que
f: P1(R) ----> S1
e^io -----> e^2io (ou o=theta, varie de O inclus à pi exclu) ?
ou je me plante ?
Merci !
Droite projective réelle et le cercle unité
2 messages
- Page 1 sur 1
bjr,
l'application
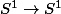
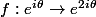
est bien définie (tous les nombres congrus à modulo
modulo  donnent la même image).
donnent la même image).
Elle est continue.
c'est un morphisme de groupes multiplicatifs.
Elle passe au quotient en une application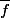 par la relation d'antipodie, qui s'exprime par
par la relation d'antipodie, qui s'exprime par
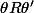 ssi
ssi )
 \rightarrow S^1)
est continue et bijective.
Soit O un ouvert de) . Son complémentaire est un fermé du compact
. Son complémentaire est un fermé du compact ) , donc un compact, l'image de
, donc un compact, l'image de 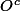 par
par 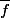 est un compact car
est un compact car 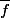 est continue,donc un fermé
est continue,donc un fermé
(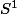 est séparé).
est séparé).
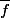 est ouverte et sa bijection réciproque continue.
est ouverte et sa bijection réciproque continue.
l'application
est bien définie (tous les nombres congrus à
Elle est continue.
c'est un morphisme de groupes multiplicatifs.
Elle passe au quotient en une application
est continue et bijective.
Soit O un ouvert de
(
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
