Double orthogonal de F = F ?

[Wenneguen]

Bonjour,

dans mon cours il est dit :

" Soit F un s.e.v de E. Si F et G sont supplémentaires orthogonaux, alors et . "

est un espace vectoriel de dimension quelconque.

Est-ce vrai dans tous les cas où une condition de dimension finie sur F par exemple est-elle requise ?


Merci ! :we:

[lionel52]

Il me semble que F doit être de dimension finie pour que ça fonctionne.
Ca marche bien dans un espace de Hilbert par contre, où l'hypothèse F fermé suffit (si F non fermé : ort(ort(F)) = fermeture de F )




edit : je retire ce que j'ai dit : Si F et G sont supplémentaires orthogonaux (hypothèse de l'énoncé alors par définition ton résultat est vrai)
cependant ce que je voulais dire c'est que dans le cas général F doit être de dimension finie pour assurer l'existence d'un supplémentaire orthogonal (ou F fermé dans un Hilbert)

[Wenneguen]

Après consultation d'un livre, il semblerait que F puisse être de dimension quelconque... :hein:

En effet je trouve dans un paragraphe dont l'introduction est " On revient au cas d'un espace préhilbertien réel quelconque ", la proposition :

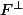
" Si F admet un supplémentaire orthogonal, admet aussi un supplémentaire orthogonal et "

[lionel52]

Oui oui c'est vrai! Si F admet une supplémentaire orthogonal G alors par définition F est le supplémentaire orthogonal de G aussi lol