Bonjour à vous,
J'ai un petit problème sur les égalités (double inclusion ou pas):
J'ai deux exercices qui cherchent à démontrer une égalité et sur le premier, la correction montre l'égalité tout simplement, sur le deuxième, on montre la double inclusion (A C B et B C A) (avec C = inclu dans) :
1er exo :
Soient E, F et G trois R-espaces vectoriels, f appartient à L(E,F) et g appartient à L(F,G). Montrer que :
1) Ker(gof) = f^(-1)(Ker(g)).
2) Im(gof) = g(Im(f)).
Là on developpe un peu ce que donne Ker(gof), puis on developpe un peu ce que donne f^(-1)(Ker(g)), et on voit qu'ils sont égaux => Simple égalité.
Pour le deuxième exo :
Soient E un K-ev, p un projecteur (c'est à dire p appartient à L(E) et p² = p où p² = pop) avec id qui est l'endomorphisme de E.
1) Montrer que Im(id-p) = Ker(p).
Et là, correction :
On part de Ker(p) et on montre que c'est égal à Im(id-p), puis on part de Im(id-ip) et on montre que c'est égal à Ker(p) => double inclusion.
Quand est-ce que l'on doit considérer l'égalité comme une double inclusion, et l'égalité comme une simple égalité ? :/
Merci d'avance
Double inclusion, pas double inclusion :/
5 messages
- Page 1 sur 1
Raisonner par égalité c'est faire une double inclusion masqué.
Ca marche quand le cas est suffisamment simple pour écrire un raisonnement qui montrer les deux inclusions d'un coup.
Comem lorsque tu montres des propriétés, mettons que tu compare A et B, tu dois toujours montrer A implique B) et l'implication (inclusion) inverse.
et l'implication (inclusion) inverse.
En général tu suis un chemin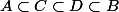
là, deux cas, soit tu peux parcourir ce même chemin en sens inverse, auquel cas tu peux raisonner par égalité (ou équivalences), soit tu peux pas et il faut faire une double inclusion non triviale.
Donc le cas d'égalité est le cas ou tu fais une double inclusion où le chemin de l'aller est l'exact symétrique du chemin de retour.
Ca marche quand le cas est suffisamment simple pour écrire un raisonnement qui montrer les deux inclusions d'un coup.
Comem lorsque tu montres des propriétés, mettons que tu compare A et B, tu dois toujours montrer A implique B
En général tu suis un chemin
là, deux cas, soit tu peux parcourir ce même chemin en sens inverse, auquel cas tu peux raisonner par égalité (ou équivalences), soit tu peux pas et il faut faire une double inclusion non triviale.
Donc le cas d'égalité est le cas ou tu fais une double inclusion où le chemin de l'aller est l'exact symétrique du chemin de retour.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
