Double inclusion
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 17 Aoû 2016, 19:42
par marawita1 » 17 Aoû 2016, 19:42
Bonsoir,
Montrer que
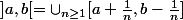
.
La deuxième inclusion est facile, mais par contre je ne peux pas prouver l'autre inclusion.
-
Robot
 par Robot » 17 Aoû 2016, 20:17
par Robot » 17 Aoû 2016, 20:17
Il suffit de prendre un x vérifiant a<x<b et de montrer qu'il existe un entier n>0 tel que a+1/n<x<b-1/n.
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 17 Aoû 2016, 21:23
par marawita1 » 17 Aoû 2016, 21:23
oui je connais le principe mais comment trouver cet entier n ????
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 17 Aoû 2016, 21:40
par Razes » 17 Aoû 2016, 21:40
Partant de
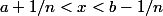
, trouve un encadrement de

en fonction de
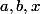
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 17 Aoû 2016, 21:52
par marawita1 » 17 Aoû 2016, 21:52
Il suffit donc de prendre un entier n vérifiant
)
.
C'est ça?
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 17 Aoû 2016, 21:57
par Razes » 17 Aoû 2016, 21:57
Oui
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 17 Aoû 2016, 22:00
par marawita1 » 17 Aoû 2016, 22:00
Merci bien.
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 18 Aoû 2016, 09:47
par marawita1 » 18 Aoû 2016, 09:47
Bonjour,
Mon amie m'a donnée une autre solution en utilisant la définition de limite d'une suite:
Puisque
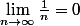
, alors
pour
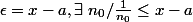
pour
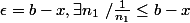
.
Donc en prenant
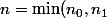)
, on trouve que
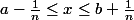
.
Que pensez-vous?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Aoû 2016, 11:04
par aymanemaysae » 18 Aoû 2016, 11:04
Bonjour,
Votre ami a vu juste :
On a
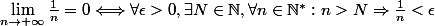
.
On prend deux valeurs particulières de

:
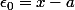
et
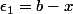
.
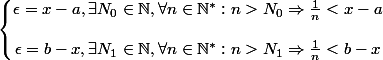
,
donc pour
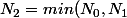)
on a

.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 18 Aoû 2016, 23:52
par Razes » 18 Aoû 2016, 23:52
Effectivement, pourquoi faire simple quand on peut faire compliqué.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités