salut tout le monde
En coordonnées cartésiennes
Soit M(x,y,z) un point de lespace dans un repère cartésien à 3 dimensions (i,j,k) On écrit OM= xi+ yj+zk
Si M se déplace en un point M MM = dOM = dxi+dyj+dyk
dxdydz est un petit volume de lespace et si un vecteur A de composante (P,Q,R) a un flux à travers les surfaces du volume, on aura divergence divA= dP/dx + dQ/dy+dR/dz
En coordonnées cylindriques
M(r,&,z) r=rayon OM &=angle z=hauteur
A(P,Q,R) on écrit divA= 1/r d(rP)/dr +1/rdQ/d& +dR/dz
Questions :
Est-ce quon pourrait écrire divA=dP/dr+dQ/rd&+dR/dz
C'est-à-dire dP/dr au lieu de 1/r d(rP)/dr
merci
Divergence en coordonnées cylindriques
12 messages
- Page 1 sur 1
divergence en coordonnées cylindriques
Salut
En coordonnées cartésiennes, on écrit div A= dAx/dx + dAy/dy + dAz/dz base (x,y,z)
En coordonnées cylindriques, on écrit div A= 1/r d(rAr)/dr + 1/r dA&/d& + dAz/dz base (r,&,z)
Question
Pourquoi par rapport à r 1/r d(rAr)/dr ?? pourquoi Ar est-il multiplié par r ? alors que r est le rayon du cercle donc une longueur et non un angle comme & ?à mon avis, par rapport à r, on aura dAr/dr + 1/rdA&/d& +dAz/dz
Autrement dit, comprends pas, pk flux de rAr à travers la surface rd&dz et non flux de Ar à travers la même surface ?
merci
En coordonnées cartésiennes, on écrit div A= dAx/dx + dAy/dy + dAz/dz base (x,y,z)
En coordonnées cylindriques, on écrit div A= 1/r d(rAr)/dr + 1/r dA&/d& + dAz/dz base (r,&,z)
Question
Pourquoi par rapport à r 1/r d(rAr)/dr ?? pourquoi Ar est-il multiplié par r ? alors que r est le rayon du cercle donc une longueur et non un angle comme & ?à mon avis, par rapport à r, on aura dAr/dr + 1/rdA&/d& +dAz/dz
Autrement dit, comprends pas, pk flux de rAr à travers la surface rd&dz et non flux de Ar à travers la même surface ?
merci
doudou63 a écrit:Salut
En coordonnées cartésiennes, on écrit div A= dAx/dx + dAy/dy + dAz/dz base (x,y,z)
En coordonnées cylindriques, on écrit div A= 1/r d(rAr)/dr + 1/r dA&/d& + dAz/dz base (r,&,z)
Question
Pourquoi par rapport à r 1/r d(rAr)/dr ?? pourquoi Ar est-il multiplié par r ? alors que r est le rayon du cercle donc une longueur et non un angle comme & ?à mon avis, par rapport à r, on aura dAr/dr + 1/rdA&/d& +dAz/dz
Autrement dit, comprends pas, pk flux de rAr à travers la surface rd&dz et non flux de Ar à travers la même surface ?
merci
Salut,
Quand on parle du gradient on parle de variation de scalaire en fonction du deplacement, d'ou le fait que ce soit df/dr et df/(r(d(teta))) avec rdeta=dl suivant le vecteur e(teta)
ca tombe bien
df.h=df/dr.dr + df/(r(d(teta))).rdteta+df/dz.dz * ou les df/dxi sont les dérivées partielles
df(h)=df.dh=df/dr.dr+df/d(teta).d(teta)+df/dz.dz
Ici pour l'operateur div, c'est pas la meme chose, ce n'est pas la derivée par rapport a un deplacement de OM c'est une sorte de dérivée du flux. Ce n'est pas la meme interpretation physique.
buzard a écrit:parce que plus généralement la divergence est définie comme la trace du gradient vectoriel (ou différentielle) du champ de vecteur :
Ca n'a rien a voir avec l'interpretation physique ca. Ca c'est juste la definition mathematiques independantes de la base (que tu as scolairement apprise). C'est pas ce qu'on te demande.
Les choses ne sont pas pareille suivant la regle (ou l'outils de mesure) que tu va utiliser, le tenseur metrique de ton système de coordonnée introduit indéniablement des modifications dans les quantités que tu mesure (résultat de la théorie de la relativité générale)
dans le cas d'un système de coordonnée cylindre, la composante radiale à une dérivation non négligeable sur l'axe transversale, et inversement. cette incidence est exactement proportionnelle au rayon.
c'est d'ailleur pourquoi l'on se retrouve avec un facteur normalisant 1/r
dans le cas d'un système de coordonnée cylindre, la composante radiale à une dérivation non négligeable sur l'axe transversale, et inversement. cette incidence est exactement proportionnelle au rayon.
c'est d'ailleur pourquoi l'on se retrouve avec un facteur normalisant 1/r
Je rappelle par exemple que si la variation scalaire vaut la somme des dérivées partielle multiplié par les deplacements correspondant, physiquement c'est parce que l'on peut representer les variations infinitesimale par plusieurs variations infinitesimale suivant les axes:
=grad(f).(h)) peut etre interpretenté comme, en 2D par exemple :
peut etre interpretenté comme, en 2D par exemple :
avec A un point de l'espace affine et h un vecteur de l'EV associé.
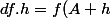-f(A)=f(B)-f(A)= (f(B)-f(C))+(f(C)-f(A))=df(BC)+df(AC)=df/dx.dx+df/dy.dy) ou C est le projeté orthogonale de B sur l'axe des x(en coordonnée cartesienne par exemple), ca s'interprettent donc comme deux deplacements suivant les axes, du coup on obtient:
ou C est le projeté orthogonale de B sur l'axe des x(en coordonnée cartesienne par exemple), ca s'interprettent donc comme deux deplacements suivant les axes, du coup on obtient: .h) .
.
Pour l'operateur div, l'intepretation physique est moins triviale, c'est en quelque sorte le flux elementaire par unité de volume: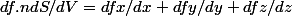 (en coordonnée cartesienne)
(en coordonnée cartesienne)
avec A un point de l'espace affine et h un vecteur de l'EV associé.
Pour l'operateur div, l'intepretation physique est moins triviale, c'est en quelque sorte le flux elementaire par unité de volume:
BQss a écrit:Pour l'operateur div, l'intepretation physique est moins triviale, c'est en quelque sorte le flux elementaire par unité de volume:(en coordonnée cartesienne)
cette unité de volume elementaire depend justement du point de mesure (qui fait varier également le vecteur), les "parois" élémentaire sont sujette aux mêmes variations qu'une surface qui gonfle (axe radiale) et une surface qui tourne (axe transversale)
la divergence c'est la propension du champ à sortir de ce volume élémentaire, seulement suivant sa direction il a plus ou moins de faciliter à le faire.
la composante axiale par exemple se confronte à la dilatation du volume, et la composante transversale à sa rotation. (dilatation et rotation qui ont intrinsequement des facteurs variant et covariant)
buzard a écrit:
la divergence c'est la propension du champ à sortir de ce volume élémentaire.
C'est exactement ce que l'interpretation du flux elementaire ( a travers une surface fermé je precise) explique, normalisé par le volume... Le bilan c'est ce qui sort sans rentrer par ailleurs... Pour un courant dans une riviere par exemple, le flux elementaire normalisé c'est la variation par rapport au temps du volume par unité de volume. Le div ce n'est rien d'autre que ca.
divergence en coordonnées cylindriques
salut
merci à vous qui mavez donné suite à mes questions en fait, 3 choses sont à retenir : la div nest pas la dérivée par rapport au déplacement mais micro-flux sur un petit volume c'est-à-dire une propension à sortir de ce volume elementaire et en coordonnées cylyndriques elle est dictée par un outil de mesure qui est le tenseur métrique en cylindrique qui va intervenir le facteur normalisant 1/r.
néanmoins, ce facteur me reste obscur
en fait, en coord cartésienne : nabla = d/dx1 e1 + d/dx2 e2 + d/dx3 e3 soit d/dxi ei
comment determiner d/dxi en coord cylindriques
on applique la règle des derivées composées xi=cartésienns et &j = cylindriques
d/dxi = d&j/dxi d/d&j
x1 = r cos&
x2 = r sin&
x3 = z
base cylind (r,&,z)
comment peut-on démontrer que:
d/dx1 = (cos&) d/dr + ( -sin& )/r d/d& + 0 d/dz??????
Je crois que la clé de toutes mes questions est là car 1/r est bel et bien multiplié par -sin& 1/r est toujours inexplicable
merci
merci à vous qui mavez donné suite à mes questions en fait, 3 choses sont à retenir : la div nest pas la dérivée par rapport au déplacement mais micro-flux sur un petit volume c'est-à-dire une propension à sortir de ce volume elementaire et en coordonnées cylyndriques elle est dictée par un outil de mesure qui est le tenseur métrique en cylindrique qui va intervenir le facteur normalisant 1/r.
néanmoins, ce facteur me reste obscur
en fait, en coord cartésienne : nabla = d/dx1 e1 + d/dx2 e2 + d/dx3 e3 soit d/dxi ei
comment determiner d/dxi en coord cylindriques
on applique la règle des derivées composées xi=cartésienns et &j = cylindriques
d/dxi = d&j/dxi d/d&j
x1 = r cos&
x2 = r sin&
x3 = z
base cylind (r,&,z)
comment peut-on démontrer que:
d/dx1 = (cos&) d/dr + ( -sin& )/r d/d& + 0 d/dz??????
Je crois que la clé de toutes mes questions est là car 1/r est bel et bien multiplié par -sin& 1/r est toujours inexplicable
merci
divergence en coordonnées cylindriques
salut
merci à vous qui mavez donné suite à mes questions en fait, 3 choses sont à retenir : la div nest pas la dérivée par rapport au déplacement mais micro-flux sur un petit volume c'est-à-dire une propension à sortir de ce volume elementaire et en coordonnées cylyndriques elle est dictée par un outil de mesure qui est le tenseur métrique en cylindrique qui va intervenir le facteur normalisant 1/r.
néanmoins, ce facteur me reste obscur
en fait, en coord cartésienne : nabla = d/dx1 e1 + d/dx2 e2 + d/dx3 e3 soit d/dxi ei
comment determiner d/dxi en coord cylindriques
on applique la règle des derivées composées xi=cartésienns et &j = cylindriques
d/dxi = d&j/dxi d/d&j
x1 = r cos&
x2 = r sin&
x3 = z
base cylind (r,&,z)
comment peut-on démontrer que:
d/dx1 = (cos&) d/dr + ( -sin& )/r d/d& + 0 d/dz??????
Je crois que la clé de toutes mes questions est là car 1/r est bel et bien multiplié par -sin&
merci
merci à vous qui mavez donné suite à mes questions en fait, 3 choses sont à retenir : la div nest pas la dérivée par rapport au déplacement mais micro-flux sur un petit volume c'est-à-dire une propension à sortir de ce volume elementaire et en coordonnées cylyndriques elle est dictée par un outil de mesure qui est le tenseur métrique en cylindrique qui va intervenir le facteur normalisant 1/r.
néanmoins, ce facteur me reste obscur
en fait, en coord cartésienne : nabla = d/dx1 e1 + d/dx2 e2 + d/dx3 e3 soit d/dxi ei
comment determiner d/dxi en coord cylindriques
on applique la règle des derivées composées xi=cartésienns et &j = cylindriques
d/dxi = d&j/dxi d/d&j
x1 = r cos&
x2 = r sin&
x3 = z
base cylind (r,&,z)
comment peut-on démontrer que:
d/dx1 = (cos&) d/dr + ( -sin& )/r d/d& + 0 d/dz??????
Je crois que la clé de toutes mes questions est là car 1/r est bel et bien multiplié par -sin&
merci
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
