Bonjour tout le monde,
Je me susi buté à un problème lors de la résolution d'un problème dans mon cours de Calcul Intégral.
Voici un lien vers l'image de la question.
https://imgur.com/a/VXHmXqN
C'est dans le contexte du repère orthonormal de Serret-Frenet.
Toute aide sera grandement appréciée!
Merci à l'avance!
Vecteurs de base en coordonnées cylindriques et sphériques
2 messages
- Page 1 sur 1
Re: Vecteurs de base en coordonnées cylindriques et sphériqu
Salut,
Pour la a)
Considérons les coordonnées cylindriques classiques) .
.
On peut réécrire l'équation du paraboloïde comme
 = r^2(1-2\sin^2\theta)=r^2\cos(2\theta)) ,
,  ,
,  .
.
Une paramétrisation de la surface en cylindriques est donc :
 \mapsto r\overrightarrow{e_r}+r^2\cos(2\theta)\overrightarrow{e_z})
avec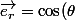\vec{e_x}+\sin(\theta)\vec{e_y}) .
.
Un vecteur normal à la surface en un point) est :
est :  .
.
On a :
\vec{e_z})
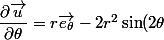\vec{e_z})
Ainsi :
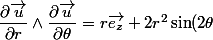\vec{e_{\theta}}-2r^2\cos(2\theta)\vec{e_r})
Je pense que tu as assez de détails pour pouvoir finaliser.
Pour la a)
Considérons les coordonnées cylindriques classiques
On peut réécrire l'équation du paraboloïde comme
Une paramétrisation de la surface en cylindriques est donc :
avec
Un vecteur normal à la surface en un point
On a :
Ainsi :
Je pense que tu as assez de détails pour pouvoir finaliser.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
