Distance p-adique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par legeniedesalpages » 04 Nov 2007, 20:59
Bonsoir, j'ai un problème avec cet exo:
On considère l'ensemble
. Soit
un nombre premier fixé;
pour tout
, on définit
)
comme étant l'exposant de
dans la décomposition en produits facteurs premier de
.
Enfin on étend cette définition aux rationnels non nuls en posant:
\in \mathbb{Z}*\times \mathbb{Z}*,\qquad \nu_p(\frac{\alpha}{\beta}) = \nu_p(\alpha)-\nu_p(\beta).)
(a) Montrer que
est bien définie sur
.
(b) Pour
, on pose:
:= \{|p^{-\nu_p(x-y)|} \mbox{ si } x\neq y\\ 0 \mbox{ si } x= y)
Montrer que
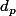
est bien une distance ultramétrique sur
.
Déjà je ne comprends pas l'utilité de la valeur absolue, dans la définition de
.
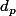
Ensuite, je patauge pour montrer l'inégalité ultratriangulaire de
:
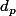
ie pour tout
,
\leq \max\ (d_p(x,y), d_p(y,z)))
.
Merci pour vos indications.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 04 Nov 2007, 21:29
Tiens tiens, quand on parle ultramétrique les valuations p-adiques sont jamais loins !!
Tout tient dans :
 \geq min(v_p(x), v_p(y)))
c'est clair dans le cas dentiers et ça se déduit dans le cas de rationnels en se ramenant à des zentiers avec
 = v_p(x) + v_p(y).)
Et oui la valeur absolue ne sert à rien.
par legeniedesalpages » 04 Nov 2007, 21:34
ThSQ a écrit:Et oui la valeur absolue ne sert à rien.
Haha.
Merci pour le tuyau, je vais chercher ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
