Valuation p-adique d'un entier naturel

[mathelot]

Bjr,


j'ai lu que si p est un entier premier,
on peut définir la norme d'un entier n par:



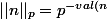où val(n) est l'exposant de p dans la décomposition de n en facteurs premiers.


qu'est ce que l'on peut prendre comme distance (p-adique) entre deux entiers ?



merci.

[yos]

C'est pas une norme, mais une valeur absolue.
(distance ultramétrique).

[ThSQ]

Si tu veux mais d(x,y) = |x-y|_p suffit !



Edit : grilled