Nombre p-adique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 16 Jan 2007, 10:26
par amine801 » 16 Jan 2007, 10:26
salut
j'ai un probleme avec un petit exo
voila l'enonce
=c_p(f_1)c_p(f_2)(-1,-1)(\sigma_1,\sigma_2).)
PS:

: le corps des nombres p-adique
)
: le symbole de Hasse de la forme f
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 16 Jan 2007, 14:28
par amine801 » 16 Jan 2007, 14:28
Dans le cas ou ca ne vous parle pas voilà une petite définition du symbole de hasse
soit f une forme quadratique a coefficient p-adique:
\\<br />c_p(f)=(-1,-1)\prod_{1\le i \le j \le n}(\alpha_i,\alpha_j))
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Jan 2007, 16:02
par yos » 16 Jan 2007, 16:02
Ta définition est valable pour f diagonale (réduite). Il faudrait peut-être diagonaliser f1 et f2 simultanément. Ce genre de chose est possible.
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 16 Jan 2007, 22:29
par amine801 » 16 Jan 2007, 22:29
on peux suposer que f1 et f2 sont diagonale de toute facons ce n'est pas la que reside la deficulte de la demonstration
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Jan 2007, 22:49
par yos » 16 Jan 2007, 22:49
Et ben... il faudrait que je relise un chapitre entier de l'arithmétique de Serre parce que là j'ai pas les idées claires. Une question cependant parce que la relation à prouver me semble bizarre : il s'agit d'une somme classique ou d'une somme directe? Autrement dit, les coefs de f+g sont les

ou bien les
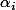 et
et les
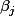
?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 16 Jan 2007, 22:57
par amine801 » 16 Jan 2007, 22:57
c'est une somme normal les deux cotes de l'egalite sont
homogene?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 16 Jan 2007, 23:35
par amine801 » 16 Jan 2007, 23:35
ah peut etre j'ai oublie de le preciser le
)
designe le symbole de hilbert
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Jan 2007, 12:34
par yos » 17 Jan 2007, 12:34
Oui je connais, il vaut 1 ou -1 selon que 0 est representé ou non par la forme x²-ay²-bz².
Le symbole de Hasse ne prend que deux valeurs également et du coup l'égalité à prouver peut sembler une banalité dans le sens ou chaque membre vaut 1 ou -1. En tout cas il peut y avoir des tas de voies pour y arriver, justement à cause de ces deux seules valeurs possibles. Un calcul direct conduit à des produits de symboles du genre
)
et que faire avec ça?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 17 Jan 2007, 12:45
par amine801 » 17 Jan 2007, 12:45
Merci de me répondre yos
je voit bien que légalité est vraie mais il me faut une démonstration
formel car c'est destine a lélaboration dun système formel est la jai du mal
a automatise cela.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités