Je voudrais montrer que
différentiable et donner sa différentielle.
Je procédé comme suivant:
Si f est différentiable, alors f(A+ H)=
En multipliant à gauche par (A + H), on a alors:
=
Donc
L'application
C'est juste ce raisonnement?
Différentiabilité de l'inverse d'une matrice
7 messages
- Page 1 sur 1
différentiabilité de l'inverse d'une matrice
par zaidoun » 24 Nov 2014, 11:59
Bonjour,
Je voudrais montrer que
) -----> M_n(\mathbb(R)))
définie par = A^{-1})
est
différentiable et donner sa différentielle.
Je procédé comme suivant:
Si f est différentiable, alors f(A+ H)=^{-1})
=  +|| H || \epsilon (H))
En multipliant à gauche par (A + H), on a alors:
 (A + H)^{-1}= I = (A +H ) ( A^{-1} + df_A(H) + ||H| \epsilon(H)))
= +HA^{-1} +o(|| H ||))
Donc +HA^{-1}=0)
, soit =- A^{-1} H A^{-1})
.
L'application
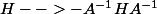
étant linéaire et par conséquent continue (dimension finie), f est bien différentiable.
C'est juste ce raisonnement?
Je voudrais montrer que
différentiable et donner sa différentielle.
Je procédé comme suivant:
Si f est différentiable, alors f(A+ H)=
En multipliant à gauche par (A + H), on a alors:
=
Donc
L'application
C'est juste ce raisonnement?
par capitaine nuggets » 24 Nov 2014, 15:31
Salut !
Ca fait 2 ans que je n'ai pas fait de calcul diff, mais le fait que tu dises direct que=(A + H)^{-1}=A^{-1} + df_A(H) +|| H || \epsilon (H))
me pose deux problèmes (après c'est peut-être moi) :
- Je pense que l'égalité^{-1}=A^{-1} + df_A(H) +|| H || \epsilon (H))
n'est pas évidente, et je voudrais savoir d'où tu la sors ;
- Ensuite, on te demande montrer que f est différentiable donc qu'il existe une application linéaire df telle que ... . Or là, tu l'utilises directement (sans savoir si elle existe)
sinon, le calcul de)
a l'air bon.
Ca fait 2 ans que je n'ai pas fait de calcul diff, mais le fait que tu dises direct que
- Je pense que l'égalité
- Ensuite, on te demande montrer que f est différentiable donc qu'il existe une application linéaire df telle que ... . Or là, tu l'utilises directement (sans savoir si elle existe)
sinon, le calcul de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par arnaud32 » 24 Nov 2014, 15:50
tu as trouve un candidat pour ta differentielle, tu dois encore verifier qu'il verifie ta relation
(A^{-1} - A^{-1} H A^{-1})=I-(HA^{-1})^2)
donc
^{-1}(I-(HA^{-1})^2)=(A+H)^{-1}-(A+H)^{-1}(HA^{-1})^2)
reste a prouver que^{-1}(HA^{-1})^2=o(||H||))
donc
reste a prouver que
par zaidoun » 24 Nov 2014, 18:24
@capitaine nuggets: J'ai supposé que f est différentiable, donc l'égalité sort de la définition d'une application différentiable.
@arnaud32: Je pense que le terme reste que tu as mentionné est un petit o de ||H||, non?
@arnaud32: Je pense que le terme reste que tu as mentionné est un petit o de ||H||, non?
par Ben314 » 24 Nov 2014, 20:03
Oui, sauf que l'énoncé était "Montrer que f est différentiable" donc si l'ensemble de ton raisonnement est basé sur un "Je suppose que f est différentiable...", j'ai peur que ça réponde pas vraiment à la question...zaidoun a écrit:@capitaine nuggets: J'ai supposé que f est différentiable, donc l'égalité sort de la définition d'une application différentiable.
Donc (bis et répétita) tout ce que tu as démontré, c'est que si f est différentiable alors sa différentielle ne peut être que blablabla et il te reste donc à montrer... que f est différentiable.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par zygomatique » 24 Nov 2014, 20:22
salut
supposer que f est différentiable pour montrer que f est différentielle .... voila qui résout bien tous les problèmes ...
posons
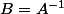
^{-1} = B(I + BH)^{-1})
alors en choisissant H" "suffisamment petit" :: ||H|| proche de 0 de façon que ||BH|| < 1 alors
^{-1} = \sum_0^{+\infty} (-1)^k(BH)^k = I - BH + (BH)^2 + ...)
la série converge normalement donc converge ... et f est différentiable ....
et donc
^{-1} ^= A^{-1} -)
...
supposer que f est différentiable pour montrer que f est différentielle .... voila qui résout bien tous les problèmes ...
posons
alors en choisissant H" "suffisamment petit" :: ||H|| proche de 0 de façon que ||BH|| < 1 alors
la série converge normalement donc converge ... et f est différentiable ....
et donc
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :