Développements limités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 16:32
par sarah79 » 15 Sep 2010, 16:32
Bonjour,
je suis en L2 de mathématiques et je rencontre quelques difficultés. Voici l'énoncé :
Déterminer si elle existe la limite quand x tend vers 0 de la fonction suivante :
f(x)= [ln(cos(3x))] / sin²(2x)
on sait que :
cos x équivaut a 1 au voisinage de 0.
J'ai posé X=3x et lim cos(3x) qd x tend vers 0=lim cos(X) qd x tend vers 0 =1
donc cos(3x) équivaut à un au voisinage de 0.
Je bloque avec le "ln" après, je ne sait pas comment faire?
J'ai aussi montré que sin(2x)équivaut à 2x au vois. de 0 mais je ne sais pas comment faire pour sin²(2x)?
Pouvez vous m'aider svp?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Sep 2010, 17:06
par Arnaud-29-31 » 15 Sep 2010, 17:06
Bonjour,
Comme l'indique ton titre, il faut faire un développement limité, dans un premier temps de cos(x) et ensuite du ln.
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 17:07
par sarah79 » 15 Sep 2010, 17:07
c'est a dire?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Sep 2010, 17:11
par Arnaud-29-31 » 15 Sep 2010, 17:11
Si tu prends un simple équivalent, tu as cos x équivalent à 1 et tu te retrouves bloquée pour trouver un équivalent de ln(cosx).
Dans ce genre de cas, on écrit le développement limité.
Quel est le développement limité en 0 de cos(x) ?
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 17:19
par sarah79 » 15 Sep 2010, 17:19
cox x = 1-(x²/4)+x^4/16+ox^n
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Sep 2010, 17:48
par Arnaud-29-31 » 15 Sep 2010, 17:48
Non ce n'est pas ça.
On peut s'arrêter à l'ordre 2
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 17:53
par sarah79 » 15 Sep 2010, 17:53
pourquoi?
je ne comprend pas. on a vu dans le cours que ln(1+x) équivaut a x au voisinage de 0.donc je suppose qu'il faut trouvé quelque chose de la forme ln(1+...)
Mais la moi j'ai ln(cos(3x))?
jsais pas comment faire, on peut pas dire que cos(3x)=cos(2x+x) et développé comme ça?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Sep 2010, 18:31
par Arnaud-29-31 » 15 Sep 2010, 18:31
Non le DL de cos x donne bien 1+ ... donc avec ca on peut ensuite faire un DL du ln.
Mais je répète : ton DL de cos x n'est pas bon.
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 18:45
par sarah79 » 15 Sep 2010, 18:45
DONC cos x =1-x²/4 c'est ça?
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 18:58
par sarah79 » 15 Sep 2010, 18:58
et après je fais comment pour passer de cos x à cos(3x)?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 15 Sep 2010, 20:01
par girdav » 15 Sep 2010, 20:01
Le changement de variable
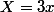
est licite, puis tu fais un dl de
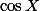
.
-
sarah79
- Membre Relatif
- Messages: 187
- Enregistré le: 06 Avr 2010, 13:13
-
 par sarah79 » 15 Sep 2010, 20:27
par sarah79 » 15 Sep 2010, 20:27
girdav a écrit:Le changement de variable
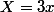
est licite, puis tu fais un dl de
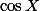
.
Donc je peux écrire :
sachant que cos x =1-x²/4, on pose X=3x et on a cos X=1-X²/4 et donc on a :
ln(cos(3x))= ln (1-X²/4) et on trouve ln(1-X²/4) equivaut à -X²/4 au voisinage de 0. C'est ça?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 15 Sep 2010, 20:57
par girdav » 15 Sep 2010, 20:57
Attention, il ne faut pas oublier le petit o. Après, on utilise la composition des développement limités. Il faut faire attention à la puissance dans le petit o.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 16 Sep 2010, 16:59
par Arnaud-29-31 » 16 Sep 2010, 16:59
Encore une fois, ton développement limité de cos(x) n'est pas bon.
cos(x) = 1 - x²/2 + o(x²)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
