Bonsoir à tous, je rencontre quelques problèmes pour résoudre certains exercices sur les DLs à savoir:
1 - Le développement limité de sin(x) sur le polycopié est au rang 2n+1.
j'ai du mal à utiliser cette formule et je bidouille pour trouver les résultats.
exemple: pour le DL limité en 0 à l'ordre 3 ( en zéro ) je pose
sin(x) = x - x3/3! + o(x3) (x3 = x^3 )
pour un DL à l'ordre 4 " je m'arrete " à ce que l'on mettrai pour un DL à l'ordre 3 ( je prend le DL du nombre impair inférieu ), donc la même chose: est-ce juste? En pratique oui mais je voudrais une confirmation!
Pareil pour le cos(x)
2 -Je n'ai pas compris la correction du DL limité de e^cos(x) en zéro à l'ordre 3,
ni celui de aux mêmes conditions ( a^x + b^x / 2 ) ^ 1/x
Si l'un dentre vous me donne toutes les étapes détaillés du développement des ces deux là il gagnerait ma reconnaissance éternelle. En effet, j'ai déja beaucoup cherché , j'ai le corrigé sous les yeux et je ne comprend pas les rapports entre certaines lignes. Cela m'aiderai beaucoup si vous me montriez toutes les étapes ( je sais que ce n'est pas votre politique, mais je galère vraiment ... )
:salut:
Développements limités quelques questions
9 messages
- Page 1 sur 1
Rebonjour,
Dans un autre exercice sur les Dls, je suis amené à calculer le développement limité à l'ordre 2 de

Je calcule dabord celui de
Ce qui correspond à^{\frac{1}{2}})
Sachant que je sais que le DL de^\alpha = 1+\alpha.X+\frac{\alpha(\alpha -1)}{2!}X^2 + o(X^2))
On a alors^ {\frac{1}{2}}<br /> = 1+\frac{1}{2}<br />X+\frac{\frac{1}{2}<br />(\frac{1}{2}<br /> -1)}{2!}X^2 + o(X^2))
Je développe^ {\frac{1}{2}}<br /> = 1+\frac{1}{2}X +\frac{-1}{8}X^2 <br /> + o(X^2))
Je remplace par
par 
Ce qui donne)
avec l'inverse au final je trouve)
Ce qui est faux car d'après la correction je devrais trouver)
J'ai fait une connerie mais où ? Si une âme généreuse pouvait m'aider.... :hein: :hein:
Dans un autre exercice sur les Dls, je suis amené à calculer le développement limité à l'ordre 2 de
Je calcule dabord celui de
Ce qui correspond à
Sachant que je sais que le DL de
On a alors
Je développe
Je remplace
Ce qui donne
avec l'inverse au final je trouve
Ce qui est faux car d'après la correction je devrais trouver
J'ai fait une connerie mais où ? Si une âme généreuse pouvait m'aider.... :hein: :hein:
Salut,
Est tu vraiment bien sûr que l'inverse de a+b+c est 1/a+1/b+1/c, c'est à dire que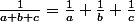 ?
?
Ta méthode marche, mais pour évaluer l'inverse de) , il faut dire que cet inverse est de la forme
, il faut dire que cet inverse est de la forme  où
où ) tend vers 0 lorsque U tend vers 0 ce qui signifie qu'on peut utiliser le D.L. en 0 de
tend vers 0 lorsque U tend vers 0 ce qui signifie qu'on peut utiliser le D.L. en 0 de  pour conclure.
pour conclure.
Sinon, il aurrait été beaucoup plus simple de partir de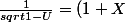^{\alpha}) où
où 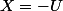 et
et 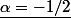 !!!!
!!!!
Est tu vraiment bien sûr que l'inverse de a+b+c est 1/a+1/b+1/c, c'est à dire que
Ta méthode marche, mais pour évaluer l'inverse de
Sinon, il aurrait été beaucoup plus simple de partir de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
