Développement décimal d'un nombre rationnel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
daxamo
- Messages: 4
- Enregistré le: 30 Sep 2015, 18:54
-
 par daxamo » 30 Sep 2015, 19:06
par daxamo » 30 Sep 2015, 19:06
Bonjour,
Je revois mes cours de maths, et je maperçois que certaines choses me bloquent. Il y a quelques formules sur ce chapitre, cependant la première formule ne me semble pas intuitive (le reste passe !).
Je vous donne un exemple, on a :
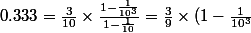 = \frac{1}{3} \times (1- \frac{1}{10^3}))
Le résultat est bien 0.333 mais je ne comprends pas le développement ! Si vous pouviez m'éclairer

.
Merci !

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Sep 2015, 19:13
par zygomatique » 30 Sep 2015, 19:13
0,3 + 0,03 + 0,003 + ... + 0,0000000000....00003 est la somme des termes d'une suite géométrique de raison .... ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
daxamo
- Messages: 4
- Enregistré le: 30 Sep 2015, 18:54
-
 par daxamo » 30 Sep 2015, 19:30
par daxamo » 30 Sep 2015, 19:30
J'ai vu que j'avais zappé 2 étapes. J'ai édité le post de départ.
Ce que je cherche à savoir c'est le raisonnement du développement, je ne vois pas comment on passe de ça à ça puis de ça à ça.
Est-ce que cette formule est bonne uniquement pour les suites 0.111 0.222 0.333 ou les suites par exemple 0.142857... marcheraient ? Si oui, quel facteur ?
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 01 Oct 2015, 07:59
par nodjim » 01 Oct 2015, 07:59
Peux tu préciser ce que tu ne comprends pas, on ne sait pas trop à quoi se réfère ton dernier message ?
Attention, un nombre décimal est un entier divisé par une puissance de 10.
Un nombre rationnel est une fraction.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Oct 2015, 09:56
par Doraki » 01 Oct 2015, 09:56
C'est vraiment une manière tordue de dire que 0.333 = 333/1000

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Oct 2015, 17:15
par zygomatique » 01 Oct 2015, 17:15
certes mais le pb n'est pas de dire ce que tu dis mais l'application d'une propriété ou théorème à un exemple concret mais trivial pour en justifier son artificielle utilité dans le cas présent ... mais le point de départ à une réflexion plus approfondie qui conduit à la généralisation que j'ai écrite ...
il faudrait évidemment préciser le contexte de cet exemple ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
daxamo
- Messages: 4
- Enregistré le: 30 Sep 2015, 18:54
-
 par daxamo » 01 Oct 2015, 18:33
par daxamo » 01 Oct 2015, 18:33
Le contexte ? Aucun.
J'ai donc eu le contrôle, l'exemple était sur 0.181818...18, j'ai donc réussi en me souvenant de la formule, mais je ne comprends toujours pas le raisonnement ! Je ne comprends pas les étapes du passages de 0.333 à la deuxième égalité puis à la troisième.
Mais cette formule ne marche que pour les valeurs répétitives et fixes (càd 0.111, 0.222, 0.333, ...) quand est-il des nombres du genre 0.142857... ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Oct 2015, 19:07
par zygomatique » 01 Oct 2015, 19:07
Le contexte ? Aucun.
ha bon ? tu n'as pas suivi un cours, une leçon dans lequel cet exemple a été donné ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 02 Oct 2015, 07:53
par Kolis » 02 Oct 2015, 07:53
daxamo a écrit:Le contexte ? Aucun.
J'ai donc eu le contrôle, l'exemple était sur 0.181818...18, j'ai donc réussi en me souvenant de la formule, mais je ne comprends toujours pas le raisonnement ! Je ne comprends pas les étapes du passages de 0.333 à la deuxième égalité puis à la troisième.
Mais cette formule ne marche que pour les valeurs répétitives et fixes (càd 0.111, 0.222, 0.333, ...) quand est-il des nombres du genre 0.142857... ?
Pour ce dernier exemple :

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
