Bonjour,
j'aimerais connaitre la méthode pour déterminer le plan de symétrie de la surface d'équation :
z = ;)4,5y² + 4y + xy ;)4,5x² + 4x ;) 4.
J'ai d'ores et déjà montré que z<0.
merci d'avance pour vos pistes.
Déterminer un plan de symétrie pour la surface déquation z = f(x, y)
9 messages
- Page 1 sur 1
Dans l'exemple donné, on a le plan (P): x=y
si le repère de référence est)
on prend)
avec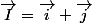 et
et 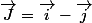
car) est un repère de (P)
est un repère de (P)
on pose
+Y(\vec{i}-\vec{j})+Z\vec{k}=x\vec{i}+y\vec{j}+z\vec{k})
Dans l'équation de la surface, on remplace ,
,  et
et  par
par 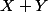 ,
, 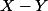 et
et  .
.

^2 +4(X-Y)+X^2-Y^2-4,5(X+Y)^2+4(X+Y)-4)

et on voit que si (X,Y,Z) appartient à la surface, il en est de même pour (X,-Y,Z) d'où la symétrie par rapport au plan passant par O et dirigé par et
et 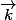
si le repère de référence est
on prend
avec
car
on pose
Dans l'équation de la surface, on remplace
et on voit que si (X,Y,Z) appartient à la surface, il en est de même pour (X,-Y,Z) d'où la symétrie par rapport au plan passant par O et dirigé par
stephaneenligne a écrit:Merci pour ton détail ; j'avais bien vu que x et y jouaient des rôles symétriques dans l'expression initiale, mais ma question serait, sur une expression quelconque, comment déterminer l'équation du plan de symétrie sous la forme ax+by+cz+d=0?
merci pour ta contribution.
A tout hasard, regarde ici
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
