j'espère qu'à plusieurs , on va y arriver!!
Les difficultés viennent de l'argument et pas du module.
Question module

en ce qui concerne l'argument:
le problème est le suivant, la quantité Arg(z) est multivaluée,
sur R+ , elle vaut 0 et vaut également

Pour définir une fonction , on ôte R+ du domaine de définition,
donc


est un ouvert étoilé par rapport à z_0=-1
pour tout z de Oméga, le segment de droite [-1,z] est inclus dans

Les ensembles du plan étoilés sont simplement connexes.
On part de
+\pi)
qu'on différentie

Cette différentielle est fermée. Le cours dit que une forme différentiellee fermée
,définie sur un ouvert simplement connexe, est exacte; elle admet une primitive
= \theta = \pi + \int_{\gamma} \, \frac{xdy-ydx}{x^2+y^2}) (1)
(1)
étant la paramétrisation du segment de droite [-1;z]
donc nous avons une (vraie) fonction
Arg(z) définie sur

à valeur dans
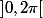
définie par (1).
On pose alors
}{2}}) (2)
(2)si
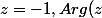=\pi ; r_2(z)=i)
j'ai un peu oublié.. si tu veux avoir les idées claires, consulte
"théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes"
de H.Cartan chez Hermann qui date de 1961
L'idée, c'est qu'en situant l'ensemble de définition sur une surface de Riemann
(le plan s'enroulant au tour de l'origine comme ces descentes en hélices de parking à plusieurs étages)
on a sans doute un revêtement du plan épointé et un domaine où la fonction Arg(z))
cesse d'être multi-valuée)
n'est pas définie mais