Détermination continue de la racine n-ième

par **legeniedesalpages** » 26 Fév 2009, 12:57

Bonjour,

Sur un domaine

du plan complexe admettant une détermination continue du log, je cherche le nombre de fonctions holomorphes

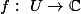
telles que

[CENTER]

.[/CENTER]

Déjà si

est une détermination du log,

convient, et en parcourant les déterminations du log, j'obtiens n déterminations de la racine n-ième.

Je ne vois pas comment obtenir autrement des déterminations de la racine n-ième, avec ou sans l'aide des déterminations du log.

Merci pour votre aide.

par **yos** » 26 Fév 2009, 16:42

Si g est une détermination du log tu as

donc en passant à l'exponentielle, f(z)=ton truc. En résumé, je dis que ton truc est nécessaire (alors que tu le dis suffisant ("convient")).
Bref, y en a pas d'autre!

par **legeniedesalpages** » 26 Fév 2009, 18:53

Bonjour yos,

comment arrives-tu à

? :hein:

par **yos** » 26 Fév 2009, 19:11

Ah ben oui il manque un 2ikpi, mais après ça marche quand même non?

par **legeniedesalpages** » 27 Fév 2009, 00:12

c'est pas clair pour arriver à cette égalité.

Par définition de

, pour

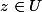
on a

, mais a t'on

?

par **yos** » 27 Fév 2009, 00:21

legeniedesalpages a écrit:a t'on ?

...

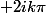
par **legeniedesalpages** » 27 Fév 2009, 23:07

ok, je n'avais pas bien compris la détermination du logarithme complexe.
Merci.

Détermination continue de la racine n-ième

détermination continue de la racine n-ième

Qui est en ligne