Bonjour,
Je dois trouver la dérivée n-ième de la fonction exp(-x²), mais j'ai écrits des pages et des pages mais sans succès, est-ce que vous pouvez m'aider ?
Dérivées successives de exp(-x²)
9 messages
- Page 1 sur 1
Re: Dérivées successives de exp(-x²)
bonjour,
Posons}=\frac{d^n}{dx^n}(exp(-x^2)))
je trouve que
}=P_n(x) exp(-x^2))
où est un polynôme de degré n, de coefficient dominant
est un polynôme de degré n, de coefficient dominant ^n) , vérifiant
, vérifiant
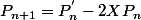
Posons
je trouve que
où
Re: Dérivées successives de exp(-x²)
Oui, mais justement, j'aurais besoin de savoir quel est justement ce fameux polynôme ?
Re: Dérivées successives de exp(-x²)
je ne sais pas, peut-être d'autres sauront.
voici les premiers:
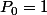
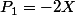
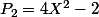
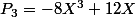
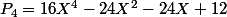
voici les premiers:
Modifié en dernier par mathelot le 20 Oct 2021, 14:10, modifié 1 fois.
Re: Dérivées successives de exp(-x²)
MERCI BCP POUR TA RÉPONSE 
Modifié en dernier par rachoid le 20 Oct 2021, 14:23, modifié 1 fois.
Re: Dérivées successives de exp(-x²)
C'est l'unique question de ton exercice ?
Concernant le "merci" de ton message précédent, j'ai un peu du mal à comprendre : tu as "noirci des pages et des pages" comme tu dit et tu n'a même pas écrit les 4 premières dérivées de f ?
Sans indiscrétion, on peut savoir ce que ça contient, "ces pages et ces pages" ?
Concernant le "merci" de ton message précédent, j'ai un peu du mal à comprendre : tu as "noirci des pages et des pages" comme tu dit et tu n'a même pas écrit les 4 premières dérivées de f ?
Sans indiscrétion, on peut savoir ce que ça contient, "ces pages et ces pages" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Dérivées successives de exp(-x²)
Non, en fait l'exercice complet, c'est :
La fonction exp(-x²) n’a pas de primitive explicite, càd, sa primitive ne peut pas être exprimée, au moyen des opérations algébriques, en termes de fonctions usuelles. Par conséquent, à toute paire (a,b)∈R², l’intégrale ∫exp(−x²)dx ne peut qu’être calculée numériquement.
a) Montrer que pour tout réel x, il existe θ∈]0,1[tel que exp(−x²)= 1−x²+((x^4)/2)-((x^6)/6)exp(−θx²).
b) En déduire une valeur approchée de l'intégrale de 0 à 1 de exp(−x²) dx et donner un majorant de l’erreur commise.
Et moi ma question, c'était pour la question a), pour pouvoir utiliser la formule de Young et trouver le développement limité de exp(-x²)
La fonction exp(-x²) n’a pas de primitive explicite, càd, sa primitive ne peut pas être exprimée, au moyen des opérations algébriques, en termes de fonctions usuelles. Par conséquent, à toute paire (a,b)∈R², l’intégrale ∫exp(−x²)dx ne peut qu’être calculée numériquement.
a) Montrer que pour tout réel x, il existe θ∈]0,1[tel que exp(−x²)= 1−x²+((x^4)/2)-((x^6)/6)exp(−θx²).
b) En déduire une valeur approchée de l'intégrale de 0 à 1 de exp(−x²) dx et donner un majorant de l’erreur commise.
Et moi ma question, c'était pour la question a), pour pouvoir utiliser la formule de Young et trouver le développement limité de exp(-x²)
Re: Dérivées successives de exp(-x²)
rachoid a écrit:Non, en fait l'exercice complet, c'est :
La fonction exp(-x²) n’a pas de primitive explicite, càd, sa primitive ne peut pas être exprimée, au moyen des opérations algébriques, en termes de fonctions usuelles. Par conséquent, à toute paire (a,b)∈R², l’intégrale ∫exp(−x²)dx ne peut qu’être calculée numériquement.
a) Montrer que pour tout réel x, il existe θ∈]0,1[tel que exp(−x²)= 1−x²+((x^4)/2)-((x^6)/6)exp(−θx²).
b) En déduire une valeur approchée de l'intégrale de 0 à 1 de exp(−x²) dx et donner un majorant de l’erreur commise.
Et moi ma question, c'était pour la question a), pour pouvoir utiliser la formule de Young et trouver le développement limité de exp(-x²)
Nom de Dieu,
Si cela avait été écrit depuis le début, je n'aurais pas cherché autant.
Je mets quand même ce que j'avais déconné, pour ne pas le mettre à la corbeille.
Tentative ... qui vaut ce qu'elle vaut.
On a : avec fn pour dérivée n ième ...
fn(x) = Pn(x) * e^(-x²)
avec fn pour dérivée n ième et Pn(x) un polynôme
En cherchant les 1ère dérivées et en "reniflant" autour des résultats, je propose une équation différentielle d'inconnue Pn, cette équation est :
(Pn)" - 2x*(Pn)' + 2n * (Pn) = 0 et si n est impair, on a Pn(0) = 0
Pour résoudre cette équation ... ce n'est pas facile.
Mon singe trouve par exemple :
pour n = 1 (donc dérivée première) : P1(x) = 2*C*x (avec C une constante qu'on pourrait calculer en se cassant la tête pour trouver une seconde condition)
Pour n = 3 (donc dérivée 3ème) : P3(x) = 4*C*x * (2x²-3)
Pour n = 5 (donc dérivée 5ème) : P5(x) = 8C*x(4(x²-5)x²+15)
...
Je vérifie en calculant les premières dérivées "à la main" :
f1(x) = -2x * exp(-x²) ---> P1 = -2x (colle avec ce qui a été trouvé par le singe avec C=-1)
f2(x) = (4x²-2).exp(-x²)
f3(x) = -4x(2x²-3).e^(-x²) --> P3 = -4x(2x²-3) (colle avec ce qui a été trouvé par le singe avec C=-1)
f4(x) = ...
f5(x) = (-32x^5+160x³-120x)*e^(-x²) (colle avec ce qui a été trouvé par le singe avec C=-1)
et donc je propose que
Avec n impair, P(n) est la solution de l'équation différentielle : P"(n) - 2x*P'(n) + 2n*P(n) = 0 avec P(0) = 0
Et pour avoir Pn(x) avec n pair, on calcule P(n-1)(x) par l'équation différentielle et on en déduit P(n) = P'(n-1) - 2x * P(n)
*****
Il faudrait trouver l'astuce qui manque pour pouvoir calculer la constante qui reste après résolution de l'équation différentielle.
 Re: Dérivées successives de exp(-x²)
Re: Dérivées successives de exp(-x²)
Merci pour vos réponses, ce n'était pas facile mais j'ai finalement trouvé la solution.
OUF ! et vivent les maths !
OUF ! et vivent les maths !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
