Dérivées partielles

[Ludo1be]

Bonjour,

Voila j'ai eu un cours sur les dérivées partielles, et j'ai loupé la base :doh:

Tout simplement...

J'ai la fonction f(x,y) = x^2-y^2
je dérive par rapport à x: Ca me donne 2x ok...

Maintenant j'ai la fonction f(x,y) = x^2.cos y
Je dérive par rapport à x, ça me donne:
-2x siny

Pourquoi dans le second exemple, je dérive aussi le terme où il y a le y alors que dans le premier exemple non?

C'est une question qui peut sembler bête mais dont j'ai un peu de mal (on a un qu'un seul cours d'une heure assez rapide sur les fonction différentiables)

[Ben314]

Maintenant j'ai la fonction f(x,y) = x^2.cos y
Je dérive par rapport à x, ça me donne:
-2x siny

Ben...., justement, ca ne donne pas ca......

[Dijkschneier]

Bonjour,

Voila j'ai eu un cours sur les dérivées partielles, et j'ai loupé la base :doh:

Tout simplement...

J'ai la fonction f(x,y) = x^2-y^2
je dérive par rapport à x: Ca me donne 2x ok...

Maintenant j'ai la fonction f(x,y) = x^2.cos y
Je dérive par rapport à x, ça me donne:
-2x siny

Pourquoi dans le second exemple, je dérive aussi le terme où il y a le y alors que dans le premier exemple non?

C'est une question qui peut sembler bête mais dont j'ai un peu de mal (on a un qu'un seul cours d'une heure assez rapide sur les fonction différentiables)

Il me semble que ton prof s'est trompé..

[Ludo1be]

Non c'est sans doute moi en recopiant sur ce forum :briques:

Je reprend un autre exemple
f(x,y) =
La dérivée par rapport à x est bien 2x...

Maintenant:
f(x,y) =
Je dérivée par rapport à x:

--> Pourquoi cette réponse et pas tout simplement ? puisque on bloque le y?

[Dijkschneier]

Puisqu'on s'intéresse à dériver par rapport à x, on considère y comme étant une constante. Du coup, cos(y) est constante, on peut alors écrire .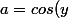
Il est maintenant possible de considérer la fonction à une seule variable : sa dérivée étant , la conclusion découle.

[Ludo1be]

Ok, donc lorsque c'est un produit, je remplace par une constante et une somme, je le bloque, concrètement?

[Ben314]

Il me semble que, dans les deux cas, tu le considère comme une constante.
La différence vient ensuite du fait (dérivées normales) que, si a est une "constante" :
La dérivée de a+f est f' (le a "disparait")
La dérivée de af est af' (le a "reste")

[Ludo1be]

Ok, merci Ben, si quelqu'un peut confirmer ;-)

[Dijkschneier]

Oui, et c'est une conséquence de la linéarité de la dérivation.