Bonjour, je bloque sur une démo:
Soient trois espaces vectoriels

,

et

et soit

une application bilinéaire de
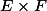
dans

. Soient

et

deux applications définies sur un intervalle ouvert

, et qui sont toutes deux dérivables en

. Alors l'application
[CENTER]

définie par
(x)=B(f(x),g(x)))
[/CENTER]
est la composée des deux applications suivantes
[CENTER]

.[/CENTER]
Comme

est dérivable en tout pont de
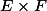
, la fonction
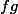
est dérivable en

et sa dérivée est l'application linéaire suivante de

dans

[CENTER]
,g'(a)h)+B(f'(a)h,g(a)))
.[/CENTER]
Comme h est réel, on peut le sortir des parenthèses et on a:
[CENTER]
'(a)=f(a)g'(a)+f'(a)g(a))
.[/CENTER]
Déjà je ne vois pas comment déterminer la dérivée de l'application:
(x)=(f(x),g(x)))
au point

.
Merci pour vos indications.
