Bonjour,
je n'arrive pas à calculer la dérivée partielle d'ordre 2 d'une composée. Pouvez-vous m'éclairer sur un exemple tiré d'un livre ? Le voici :
Soit

l'application définie sur

par :
 \in \mathbb{R}^2)
,
 = (u,v) = (2x+y,2x-y).)
La fonction

est linéaire, bijective elle définit un
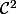
-difféomorphisme de

sur

.
Soit

la fonction définie sur

par

(

est l'inconnue d'une équation aux dérivées partielles que je ne prends pas la peine de citer).
En utilisant les formules de dérivation d'une composée, il vient :

, soit

( jusque là je comprends, je connais cette formule de " règle de la chaîne " ).
D'où :

Par contre là je ne vois pas bien comment on obtient cette expression de

... Je me doute qu'il faut réutiliser cette formule de " règle de la chaîne " à
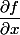
pour l'obtenir, mais je ne vois pas bien comment.
Merci de m'éclairer ! :we:
