Bonjour ! :)
J'ai la densité jointe suivante : f(x,y) = e^(-x^2*y) si x >= 1 et y >= 0, 0 sinon.
Je dois retrouver les fonctions de densité individuelles, f(x) et f(y). Pour f(x) tout va bien, mais pour f(y) j'ai l'impression que l'intégrale n'existe pas, y a-t-il un moyen de trouver f(y) malgré tout ?
Densité jointe vs densité simple
10 messages
- Page 1 sur 1
Je ne comprends pas ce que tu essaies de me dire. ^^'
ReM
Sylviel a écrit:quel est l'expression (avec intégrale) de f_Y(y) ?
Et on n'occulte pas le paramètre t conditionnant la valeur de cette intégrale.
arnaud32 a écrit:pourtu as
pour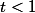
pourtu as
pour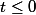
Donc je dois laisser ma réponse sous cette forme ? D'où tires-tu la borne racine de t ? Et comment puis-je tester l'indépendance des deux variables avec une densité pareille ? Je suis désolé je n'ai encore jamais vu le sujet donc je suis complètement perdu. ^^
plikskin a écrit:Donc je dois laisser ma réponse sous cette forme ? D'où tires-tu la borne racine de t ? Et comment puis-je tester l'indépendance des deux variables avec une densité pareille ? Je suis désolé je n'ai encore jamais vu le sujet donc je suis complètement perdu. ^^
Hello,
La racine est issu du changement de variable x' = x*racine(t).
Si ton but est ensuite de tester l'independance des variables, tu n'es pas obligé d'utiliser ces densités simples (mais tu pourrais, en montrant (ou non) que E[f(X)g(Y)]=E[f(X)]E[g(Y)] avec f et g des fonctions vérifiant je ne sais plus quels critères) mais en l'occident ici tu n'as pas besoin.
Dans le cas de variables à densité une autre caractérisation de l'indépendance est qu'elles sont indépendante ssi il existe g et h des fonctions telles que
f(x,y)=g(x)h(y) (tu peux décomposer ta densité jointe en produits de deux densité).
Comme tu as des fonctions bien régulières et dérivables dans ton exemple, tu peux du coup remarque que si les variables sont indépendantes, tu auras donc :
et donc en faisant le ratio des deux équation précédentes tu obtiens :
Donc si X et Y sont indépendantes, cette fonction
Fais le calcul et tu verras que ce n'est pas le cas du tout dans ton exemple..
Damien
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
