Démonstration d'implication et définition des variables

[jygl]

Bonjour

Je viens poser une question concernant une démonstration d'un implication.

Soit une propriété portant sur un n-uplet .

On nous dit que pour démontrer , il fallait commencer par :
"Soit " et non par "Soit " (notez le )

Pourriez vous me préciser pourquoi ?

Apparemment, démontrer en supposant et en partant de reviendrai à prouver l'implication pour des valeurs particulières de : c'est ça que je n'ai pas compris...

Merci pour votre aide

[Ben314]

Salut,
Bon, ben rien que la façon dont tu exprime les trucs donne l'impression que c'est pas du tout clair dans ta tête.
"démontrer que P_n implique P_{n-1}", texto, ben ça veut pas dire grand chose.
Tu dit toi même que P_n c'est une propriété qui dépend de (x1,x2,...xn) donc évidement, le fait que Pn soit vrai ou pas dépend des valeurs de (x1,x2,...xn). Idem pour P_{n-1} dont la véracité dépend de (x1,x2,...x_{n-1}) et ça signifie bien entendu que la véracité de l'implication Pn => P_{n-1} ben elle va (à priori) dépendre de x1,x2,...xn.

Bref, ce que je suppose qu'on te demande de démontrer, c'est pas que P_n => P_{n-1}, mais plutôt que
pour tout (x1,x2,...,xn) dans R^n, on a Pn(x1,x2,...,xn) => P_{n-1}(x1,x2,...,x_{n-1})
ça peut te sembler se "l'enc... de mouches", mais il faut bien être conscient que si tu commence à écrire simplement "chat noir" alors que ce qu'on t'a dit de montrer, c'est que "tout les chats du quartier sont noir", ben tu va rapidement plus rien comprendre à ce que tu écrit et rien comprendre à ce qu'on te demande de montrer (et ça, c'est 30 ans d'expérience de prof. qui te parlent...)

Ensuite, de façon quasi-systématique en math, pour montrer que "tout les trucs sont machins", intellectuellement parlant, ce qu'on fait, c'est effectivement de prendre UN truc (et un seul) et on montre que CE truc est effectivement machin. Et ça permet de conclure vu que le truc qu'on a pris, c'est en fait n'importe lequel (là faut faire super gaffe à vérifier que dans la preuve on a pas utilisé le fait qu'il est non nul, ou positif ou n'importe quoi de particulier) donc on a en fait bien montré que n'importe quel truc est machin, c'est à dire que tout les trucs sont machin.

Et dans ton cas à toi où tu doit prouver que pour tout (x1,x2,...,xn) dans R^n, on a Pn(x1,x2,...,xn) => P_{n-1}(x1,x2,...,x_{n-1}), ben tu va à priori commencer ta preuve par du : Soit (x1,x2,...,xn) un élément quelconque de R^n
Mais évidement, il peut y avoir des "variantes" : si en fait dans tout le début de ta preuve le xn n'apparait nulle part, ben tu peut évidement commencer par du : Soit (x1,x2,...,x_{n-1}) un élément quelconque de R^{n-1} puis écrire plus tard (au moment ou tu en as besoin) Soit x_{n} un élément quelconque de R.
Ca change évidement rien du tout, mais ça peut éventuellement rendre la preuve plus facile à comprendre.

En résumé, sans conteste supplémentaire (i.e. sans savoir qui est cette fameuse proposition P_n), ben je vois aucune raison valable de commencer la preuve par du Soit (x1,x2,...,x_{n-1}) un élément quelconque de R^{n-1}

EDIT : Encore que vu tes lacunes en terme d'utilisation des quantificateurs, je vois aussi une autre éventualité, à savoir que le truc que tu aie à démontrer soit :
(x1,x2,...,xn) dans R^n, Pn(x1,x2,...,xn)(x1,x2,...,x_{n-1}) dans R^{n-1}, P_{n-1}(x1,x2,...,x_{n-1}
Ce qui n'est évidement pas du tout la même chose que ce que j'ai écrit plus haut.

[jygl]

Oui je l'accorde c'est pas du tout clair dans ma tête...

De plus, moi qui voulait simplifier ma question, je vois que ça ne mène à rien. Au temps pour moi

Voici l'énoncé, je me reprend,

Soit la propriété suivante :



Démontrer que


Et pour reprendre ce que je disais, on m'a expliqué que commencer sa preuve par

"Soit vraie. Soit ..."

Alors notre conclusion sera fausse parce que aura prouvé notre implication pour des valeurs particulières de

C'est ce que je n'ai pas compris...

J'espère avoir été plus clair

[Ben314]

O.K.
Donc y'a une bonne partie de mon laïus qui est pas adapté vu que ton truc, c'est ce que j'ai mis dans l'EDIT à la fin.

Mais c'est quand même en grande partie de ta faute : tu as écrit en noir sur blanc que tu avait une proposition P_n qui dépendait de (x1,x2,...,xn) alors que c'est faux :
La proposition est effectivement une proposition qui dépend de x1,x2,...,xn, mais par contre la proposition , elle, elle dépend pas du tout de x1,x2,...,xn.

Pour que ce soit bien clair dans ta tête que c'est pas du tout la même chose, prenons un truc concon en Français :
L'affirmation "le chat est gris" c'est une affirmation qui dépend du chat considéré : vrai pour certain chats et faux pour d'autre. Alors que l'affirmation "tout les chats sont gris" ça, c'est pas du tout affirmation qui "dépend du chat" c'est une affirmation qui ne dépend de rien du tout et qui est fausse (il est bien clair qu'il existe des chats qui ne sont pas gris). Et évidement, pour rester dans la lignée, l'affirmation "tout les chats de la ville sont gris", elle ne dépend pas du chat, mais par contre elle dépend de la ville.
Donc pour en revenir au maths, un truc du style c'est une proposition qui dépend de l'ensemble A, du réel M, mais absolument pas du réel x. Et c'est pour ça que si cette affirmation est vrai, ben on dit que "A est majoré par M" ; phrase en Français dans laquelle apparait A et M, mais évidement pas x vu que la phrase ne dépend pas de x.

Bon, revenons à nos moutons : ta proposition , elle dépend donc de et d'absolument rien d'autre.
Tu doit montrer que .
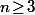
- Donc tu commence par considérer UN entier (comme c'est n'importe lequel, ça sera vrai pour tous)
- Ensuite, tu suppose que la propriété est vraie, donc en fait tu suppose que

et il faut bien comprendre que pour le moment, tu n'a absolument pas choisi de x1,x2,...,xn et tu n'a pas à en choisir vu que le but n'est pas du tout de démontrer l'affirmation çi dessus : elle est supposée vrai.
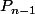
- Enfin, ce que tu doit démontrer, c'est que la proposition est elle aussi vraie, c'est à dire que tu doit démontrer que

Et là, effectivement, pour démontrer que ce truc qui commence par du est vrai, tu va commencer par dire que tu considère (ou si tu préfère que tu choisi) un élément .
Et là où il y a un problème (et à mon avis au fond c'est ça qui t'embrouille), c'est que les mêmes lettres , on s'en est servi pour deux chose essentiellement différentes, à savoir énoncer l'hypothèse (H) que l'on avait, mais aussi pour énoncer la proposition (D) que l'on avait à démontrer et c'est à peu près sûr qu'on va se mélanger les pinceaux... 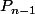Donc arrivé à ce point, ben on prend du blanco et on écrit que ce qu'on doit démontrer, c'est la proposition qui dit que :

(évidement on pourrait à la place remplacer les x par des y dans l'hypothèse : le tout c'est de pas avoir les même lettres)
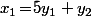
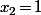
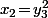
Ensuit, on écrit qu'on considère un élément et on essaye de montrer l'inégalité en question sachant qu'on a le droit de se servir de l'hypothèse, mais qu'on peut évidement s'en servir e prenant par exemple ; ; etc...
En fait, ben on peut prendre n'importe quoi pour les pourvu bien entendu qu'ils soient strictement positifs vu que notre hypothèse dit .

C'est plus clair comme ça ?

[jygl]

Ok je n'ai pas était clair, pour moi dire que portait sur mon n-uplet sous entendait
Mea culpa

Du coup merci d'avoir pris le temps de me répondre !
C'est en fait cette partie qui m'a éclairée :

Bon, revenons à nos moutons : ta proposition , elle dépend donc de et d'absolument rien d'autre.
Tu doit montrer que .
- Donc tu commence par considérer UN entier (comme c'est n'importe lequel, ça sera vrai pour tous)
- Ensuite, tu suppose que la propriété est vraie, donc en fait tu suppose que

et il faut bien comprendre que pour le moment, tu n'a absolument pas choisi de x1,x2,...,xn et tu n'a pas à en choisir vu que le but n'est pas du tout de démontrer l'affirmation çi dessus : elle est supposée vrai.
- Enfin, ce que tu doit démontrer, c'est que la proposition est elle aussi vraie, c'est à dire que tu doit démontrer que

Et là, effectivement, pour démontrer que ce truc qui commence par du est vrai, tu va commencer par dire que tu considère (ou si tu préfère que tu choisi) un élément .

Je me rend compte, bien que c'était écrit explicitement sur le sujet, que dans ma tête je considérer juste l'inégalité , et oubliant le qui va avec.

Évidemment vu comme ça, je comprend mieux pourquoi on pose ...

Merci beaucoup encore une fois pour ta réponse détaillée !

Pour l'instant je vais considère que j'ai compris, je me repencherai dessus demain pour vérifier que ça soit clair pour moi.