Démonstration formule de Grassmann

[Bizarre]

Bonsoir à tous,

Je cale sur une démonstration de la formule de Grassmann. Je sais qu'il y en a une autre connue, faisant appel aux supplémentaires, mais j'aimerais comprendre celle-ci. La plus proche que j'ai trouvée de celle de mon cours est ici:

http://alainguichet.mathematex.net/ecs-touchard/wiki/doku.php?id=math:2:5_1_2:grassmann

Ce que je ne saisis pas bien, c'est "Alors, dans le vecteur de gauche, on en déduit que les mu sont tous nuls (puisque truc est une base de F) et que les nu sont tous nuls (puisque truc est une base de G)."

Peut-être que ça a à voir avec l'unicité de l'écriture d'un vecteur dans une base donnée? Auquel cas je n'ai pas tout compris non plus.

Quoiqu'il en soit, je veux bien une explication détaillée si possible

Bonne soirée

[Ben314]

Salut,
Eh ben, les nom propres ont toujours autant le vent en poupe (j'avais encore jamais entendu dire qu'il s'agissait de la formule de "Grassmann")

Sinon, concernant ta question, un petit rappel : une base de "truc", c'est une famille libre (et génératrice de "truc") et c'est quoi la définition d'une famille libre ?
Et ben justement, c'est que la seule combinaison linéaire des vecteurs en question qui fait le vecteur nul, c'est celle où tout les coeffs. sont nuls.

[Bizarre]

Salut,
Eh ben, les nom propres ont toujours autant le vent en poupe (j'avais encore jamais entendu dire qu'il s'agissait de la formule de "Grassmann")

Sinon, concernant ta question, un petit rappel : une base de "truc", c'est une famille libre (et génératrice de "truc") et c'est quoi la définition d'une famille libre ?
Et ben justement, c'est que la seule combinaison linéaire des vecteurs en question qui fait le vecteur nul, c'est celle où tout les coeffs. sont nuls.

Oui, mon prof "aime" les noms propres
Et sinon, je ne vois toujours pas : là, on ne regarde pas la combinaison nulle... Peux-tu m'expliquer davantage, peut être un peu plus en amont?

Edit : ce que je veux dire, c'est que on ne peut pas déduire de Morceau 1 + Morceau 2 + Morceau 3 = 0 ou de Morceau 1 + Morceau 2 = - Morceau 3 que Morceau 1 = Morceau 2 = Morceau 3 = 0 :/

[Ben314]

Salut,
Eh ben, les nom propres ont toujours autant le vent en poupe (j'avais encore jamais entendu dire qu'il s'agissait de la formule de "Grassmann")

Sinon, concernant ta question, un petit rappel : une base de "truc", c'est une famille libre (et génératrice de "truc") et c'est quoi la définition d'une famille libre ?
Et ben justement, c'est que la seule combinaison linéaire des vecteurs en question qui fait le vecteur nul, c'est celle où tout les coeffs. sont nuls.

[Ben314]

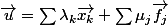
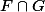
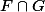
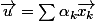
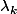
Tu sait que le vecteur est dans donc, vu que les forment une base de , il peut s'écrire sous la forme ce qui signifie que et cela prouve que les sont tous nuls (et que les sont égaux aux ).

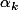
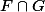
Après, je n'avais pas complètement lu ton post, mais si tu préfère (et ça revient exactement au même) tu peut directement utiliser l'unicité de la décomposition dans une base : le vecteur U çi dessus étant dans peut s'écrire uniquement à l'aide des xi, et comme les xi union les fj forme une base, il peut s'écrire de façon unique à l'aide des xi et des fj. Donc forcément les coeffs des fj seront nuls.

[Bizarre]

Merci Ben314 ;)

Je comprends mieux!

Bonne soirée