Bonjour, j'ai vu récemment dans un cours :
^{E[u(X)] = \sum_{i=1}^{+infini}{(1/2)^{i}}ln(2^{i})}
et ensuite que
E[u(X)] = ln(2) \sum_{i=1}^{+infini}{(i/2^{i}) = 2ln(2)}
je ne comprends pas les différentes étapes pour passer de l'un à l'autre puis au résultat final
Merci d'avance.
Demonstration espérance morale bernouilli
3 messages
- Page 1 sur 1
Re: demonstration espérance morale bernouilli
Du vrai code tex entre balises tex, c'est mieux !
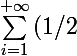^{i}}\ln(2^{i})}=\ln(2) \sum_{i=1}^{+\inftyi}{(i/2^{i}) = 2\ln(2)})
La première étape, c'est juste que=i\,\ln(2)) . La deuxième est une peu plus sioux. On utilise que pour tout
. La deuxième est une peu plus sioux. On utilise que pour tout  tel que
tel que 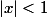 :
:
^2}= \sum_{i=1}^{+\infty} i\,x^i\;.)
On l'applique ici pour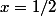 .
.
La première étape, c'est juste que
On l'applique ici pour
Re: demonstration espérance morale bernouilli
Désolé c'est mon premier message je sais pas trop comment ça marche.
Oui la première étape était facile, je ne connaissais pas la formule pour la seconde, merci beaucoup.
Oui la première étape était facile, je ne connaissais pas la formule pour la seconde, merci beaucoup.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
