Lemniscate de bernouilli

[caly]

bonjour,
j'ai un controle de maths demain ,j'essaye de faire des exo pour m'entrainer mais celui là impossible de la démarrer

voila mon soucis:

dans un repère ortho du plan,construire la courbe dont la représentation paramétrique est:
x=at/(1+t^4)
y=at^3*(1+t^4)
t E R

il est conseiller d'étudier l'effet du changement de t en 1*t dans les expression définnissant x et y

merci de m'aider mais je ne veux pas la résolution de l'exo mais seulement la méthodologie pour y arriver

[caly]

alors svp un p'tit effort un p'tit coup de pouce

[busard_des_roseaux]

Bj,

Bernouilli ne prend pas de i.

méthode:
le changement de variable indiquera, ou une symétrie, ou bien
un paramètrage "double".

Sinon, si l'on utilise la métaphore cinématique, où la variable t représente le temps et M(t) un point qui se déplace au cours du temps sur la courbe, certains paramètrages peuvent conduire à parcourir la courbe plusieurs fois.

les choses à faire sont:
1) éliminer les paramètrages qui font parcourir la courbe
plusieurs fois en restreignant le domaine de
2) dresser les tableaux de variations indépendants des
deux fonctions x(t) et y(t)
3) étudier les points doubles qui sont données par
avec
d'inconnue
4) placer les vecteurs tangents de coordonnées x'(t),y'(t)
aux points intéressants, en particulier aux points doubles.
5) faire une étude locale en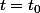
en effectuant des développements limités pour classer éventuelleemnt
les points d'inflexion ou de rebroussement.

à noter que la lemniscate de Bernoulli est une courbe mathématiquement
intéressante, il me semble qu'il y a un lien entre sa rectification (calcul
de la longueur de la courbe) et la moyenne arithmético géométrique de 1 et conduisant à des algorithmes d'approximation de (cf Friedrich Gauss, les frères Borwein..). C'était l'objet
d'un énoncé de capes d'il y a quelques années...

[caly]

merci je essayer; et désolé pour bernoulli

[busard_des_roseaux]

il est conseiller d'étudier l'effet du changement de t en 1*t dans les expression définnissant x et y

c koi comme changement de variable ?

[caly]

le changement de t en 1/t

[busard_des_roseaux]

x=at/(1+t^4)
y=at^3/(1+t^4)

re,

j'ai crû voir ce qui était demandé:

en fait, ta formule de y(t) est fausse. je l'ai corrigée:






si, à un instant , le point mobile est en
à l'instant ce même point mobile
est en où est le symétrique
de par rapport à la 1ère bissectrice, droite d'équation y=x

en effet, la symétrie orthogonale permute les coordonnées

phénomène bien connu de ceux qui tracent les courbes de fonctions réciproques.

la seconde bissectrice étant la droite d'équation y=-x

on doit pouvoir restreindre l'étude à t
puisque envoie ]0;1]
sur