Supposons qu'il existe deux décompositions primales d'un entier naturel n. Alors il existe des nombres premiers
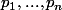
et des entiers (qui peuvent être nul :id: pourquoi ?)

tels que :
Soient

Montrons que

(les autres se font de la même façon):
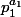
divise

. D'après le théorème de Gauss on conclut que
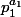
divise

.
Donc il existe un entier k tel que
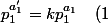)
De même,

divise

. Toujours d'après le théorème de Gauss on conclut que

divise
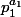
.
Donc il existe un entier k' tel que
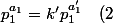)
Par produit de (1) par (2), on en déduit que

.
Donc k=1 (par positivité).
On injecte dans (1) , on obtient :

qui donne

