Définition sous groupe discret
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kagoune
- Membre Naturel
- Messages: 78
- Enregistré le: 08 Mai 2007, 10:43
-
 par kagoune » 17 Nov 2009, 14:47
par kagoune » 17 Nov 2009, 14:47
pourriez vous me donner la définition d'un sous groupe discret? merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 15:53
par Nightmare » 17 Nov 2009, 15:53
Salut !
Un ensemble est dit discret si tout ses points sont isolés (au sens où n'importe quel point admet un voisinage qui ne rencontre pas l'ensemble). Ceci revient à dire que la topologie induite sur le sous-groupe est la topologie discrète.
Par exemple les ensembles de la forme kZ sont des sous-groupes discrets de R (on peut d'ailleurs montrer qu'un sous-groupes multiplicatif de R est soit discret soit dense dans R, c'est peut être ton exercice !)
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:08
par kazeriahm » 17 Nov 2009, 16:08
Un sous groupe ... additif !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 16:11
par Nightmare » 17 Nov 2009, 16:11
Euh oui, additif, merci ! (Tu es souvent à corriger mes bourdes, je devrais t'engager pour être à mes côté pendant mes partiels, ça m'éviterait pas mal de points perdus pour ce genre d'étourderie :lol2: )
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:13
par kazeriahm » 17 Nov 2009, 16:13
Hehe
d'ailleurs quels sont les sous groupes multiplicatifs de R* ? existe-t-il une caracterisation similaire a celle des groupes additifs ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 16:24
par Nightmare » 17 Nov 2009, 16:24
Tiens je ne m'étais pas posé la question. A priori on peut les déduire de ceux de (R,+) vu que
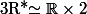
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:25
par kazeriahm » 17 Nov 2009, 16:25
:hein: Je ne comprends pas ta notation R*2
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 16:26
par Nightmare » 17 Nov 2009, 16:26
Oui mon gras n'est pas passé, je note 2 le corps à deux éléments :happy3:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:33
par kazeriahm » 17 Nov 2009, 16:33
Et tu les isomorphises (R* et Rx2) ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 16:34
par Nightmare » 17 Nov 2009, 16:34
C'est ça, R* est isomorphe à Z/2Z * R me semble-t-il !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:42
par kazeriahm » 17 Nov 2009, 16:42
Oui il semble que ca marche avec ln et exp. Bon ok soit G un sous groupe multiplicatif de R+*, c'est l'image par exp d'un sous groupe F de (R,+). Si F est dense alors G est dense all right. Si F=aZ, alors... G={exp(a*n), n entier relatif} et ce type d'ensemble c'est quoi ? Point d'accumulation ? 0 au moins
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 16:48
par Nightmare » 17 Nov 2009, 16:48
Je ne vois pas quoi dire de plus sur ces ensembles. Tu es sûr que 0 est un point d'accumulation? Ca me semble difficile !
-
kagoune
- Membre Naturel
- Messages: 78
- Enregistré le: 08 Mai 2007, 10:43
-
 par kagoune » 17 Nov 2009, 16:52
par kagoune » 17 Nov 2009, 16:52
merci! heu non ce n'est pas mon exercice... je l'ai déja fais cet exo en ne sachant pas que ça voulait dire que les sous groupes de R était soit denses soit discret, on m'avait juste demandé de démontrer que les sous groupes de R étaient soit denses soit de la forme aZ. en tout cas merci!
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 17 Nov 2009, 16:54
par kazeriahm » 17 Nov 2009, 16:54
Non mais en fait on est bete. Soit G un sous groupe multiplicatif de R+*. Soit G est dense dans R+ soit il existe a>0 tel que G={a^n, n entier relatif} Voila.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Nov 2009, 17:00
par Nightmare » 17 Nov 2009, 17:00
Oui ça c'est sûr puisque exp est un isomorphisme de R dans R+* mais je pensais qu'on s'intéressait à R* tout entier !
-
kagoune
- Membre Naturel
- Messages: 78
- Enregistré le: 08 Mai 2007, 10:43
-
 par kagoune » 17 Nov 2009, 17:33
par kagoune » 17 Nov 2009, 17:33
mais tous les sous groupes dicrets de R sont donc de la forme aZ. est il possible de le démontrer?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Nov 2009, 14:37
par kazeriahm » 18 Nov 2009, 14:37
Si G est un sous grpe de R* alors G inter R+ est un sous groupe de R+* faut voir comment faire pour prendre en compte R^-
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2009, 15:03
par Nightmare » 18 Nov 2009, 15:03
kagoune a écrit:mais tous les sous groupes dicrets de R sont donc de la forme aZ. est il possible de le démontrer?
Ce n'est pas vrai !
Par exemple Z+2Z est discret dans R mais n'est pas de la forme aZ !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 18 Nov 2009, 15:04
par kazeriahm » 18 Nov 2009, 15:04
.... ben si c'est Z
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2009, 15:08
par Nightmare » 18 Nov 2009, 15:08
kazeriahm a écrit:Si G est un sous grpe de R* alors G inter R+ est un sous groupe de R+* faut voir comment faire pour prendre en compte R^-
Re salut l'ami !
En fait je ne comprends pas, je croyais qu'on avait réglé le problème en disant que R* était isomorphe à 2xR !
Les sous-groupes de 2xR sont :
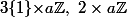
, soit

avec D sous-groupe dense dans R et évidemment il reste les cas triviaux
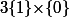
et
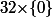
Reste à appliquer l'isomorphisme réciproque
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
