Decomposititon en element simple

[naruto-next]

Salut,

j'essaye de trouver une integrale d'une fonction , mais faut la decomposer en element simple :



ensuite :



j'essaye de trouver a ,b ,c ,d ,e mais j'ai du mal . en faite j'ai du mal avec les poles multiple donc pour trouver b et c j'arrive pas , en multipliant par x-1 je trouve b = 0 normal ? .

merci

[Carpate]

Salut,

j'essaye de trouver une integrale d'une fonction , mais faut la decomposer en element simple :



ensuite :



j'essaye de trouver a ,b ,c ,d ,e mais j'ai du mal . en faite j'ai du mal avec les poles multiple donc pour trouver b et c j'arrive pas , en multipliant par x-1 je trouve b = 0 normal ? .

merci

C'est incompréhensible, pourquoi ce terme en ?



On multiplie par x - 2 et on fait x = 2 :


On multiplie par (x - 1)^2 et on fait x = 1 :


On évalue f(0) :



Calculs à vérifier ...

[Sa Majesté]

Il en manque un bout

[Carpate]

Il en manque un bout

Exact, je suis allé un peu vite !

[naruto-next]

merci de votre aide , en faite j'ai oublié quelque chose d'important sur f(x) et j'ai mis t au lieu de x ...
ca donne



et la bah j'ai du mal a trouver b , c , d et e

[Carpate]

merci de votre aide , en faite j'ai oublié quelque chose d'important sur f(x) et j'ai mis t au lieu de x ...
ca donne



et la bah j'ai du mal a trouver b , c , d et e

On t'a déjà indiqué la méthode :
a) calcul de a :
On multiplie par x -2 et on fait x = 2


b) calcul de c :
On multiplie par et on fait


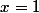
c) Calcul de d et e :
On multiplie par et on fait x = + ou - i
--> 2 relations entre d et e

d) Calcul de b :
En raison de la mutiplicité de la racine x = 1 on ne peut pas multiplier par x - 1 et faire x = 1 (il resterait un x - 1 au dénominateur)

Sachant que a,c, e sont connus, on obtient b

[naruto-next]

merci , mais j'ai pas saisie pour d et e .

[naruto-next]

Up .

svp

[MacManus]

Up .

svp

Salut,

Tu multiplies les deux membres de l'égalité par le facteur (x²+1) et tu remplaces x par i puis par -i pour obtenir un système de deux équations à deux inconnues (d et e)

[chan79]

c) Calcul de d et e :
On multiplie par et on fait x = + ou - i
--> 2 relations entre d et e

tu remplaces x par i puis par -i et avec les deux égalités obtenues, tu calcules d et e.
Par la suite, tu peux aussi étudier la limite de xf(x) quand x tend vers +inf
d'une part elle est égale à 0 et d'autre part elle est égale à a+b+d
donc a+b+d=0 ce qui te permet de trouver b