Décomposition d'un entier en une somme de factoriels

[vizcaronbis]

Bonjour tout le monde,

Je travaille actuellement sur les permutations et les mathématiques qui se cachent derrière. :mur:

Je bute sur une démonstration qui consiste à montrer que tout entier peut s'écrire sous la forme d'une somme de ak*k! (avec k>=1), chaque chiffre ak parcourant [0...k]

A la question précédente, j'ai démontré que pour tout entier n, la somme des nombres k.k!, k de 0 à n était l'entier précédant (n+1) !. Cela doit être utile.

Si quelqu'un peut m'aider, je le remercie d'avance .

[Manny06]

Bonjour tout le monde,

Je travaille actuellement sur les permutations et les mathématiques qui se cachent derrière. :mur:

Je bute sur une démonstration qui consiste à montrer que tout entier peut s'écrire sous la forme d'une somme de ak*k! (avec k>=1), chaque chiffre ak parcourant [0...k]

A la question précédente, j'ai démontré que pour tout entier n, la somme des nombres k.k!, k de 0 à n était l'entier précédant (n+1) !. Cela doit être utile.

Si quelqu'un peut m'aider, je le remercie d'avance .

Donne l'énoncé exact

[Sake]

Bonjour tout le monde,

Je travaille actuellement sur les permutations et les mathématiques qui se cachent derrière. :mur:

Je bute sur une démonstration qui consiste à montrer que tout entier peut s'écrire sous la forme d'une somme de ak*k! (avec k>=1), chaque chiffre ak parcourant [0...k]

A la question précédente, j'ai démontré que pour tout entier n, la somme des nombres k.k!, k de 0 à n était l'entier précédant (n+1) !. Cela doit être utile.

Si quelqu'un peut m'aider, je le remercie d'avance .

Salut,

Tout entier peut s'écrire sous la forme d'une somme de factorielles. En fait, tu peux n'additionner que des 1 si tu le souhaites, ces 1 pouvant s'écrire sous la forme 1*1! (et 1 est bien dans [[0,1]]). Ce cas limite étant valable pour tout entier donné, on peut conclure que pour tout entier, il existe une telle configuration d'écriture.

[Ben314]

Salut,
Déjà, ce qu'il faut comprendre, c'est que c'est un genre "d'écriture en base n!", c'est à dire que c'est relativement proche de l'écriture par exemple en base 10 où on écrit avec les .
Donc pour la preuve en question, je ferais exactement comme pour la base 10 (ou une autre base) où il y a essenciellment deux méthodes :
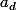a) Soit on commence par les "grands" coefficients donc on cherche d'abord le d tel que puis on prend pour le quotient de la division de n par et on poursuit en considérant le reste r de la division de n par (de façon théorique, on rédige ça en terme de réccurenc)
b) Soit on commence par les "petits" coefficients donc on dit en premier que est le reste de la division de n par et on poursuit en considérant le reste q de la division de n par .

Là, c'est (quasi) pareil.
Le seul point où il faut faire un peu attention, c'est pour justifier l'unicité de l'écriture et ça va assez clairement venir de la relation que tu as démontré précédemment qui dit qu'en ajoutant uniquement des avec et , tu ne peut pas atteindre .

Je ne te donne (volontairement) pas la solution "toute faite" pour te laisser chercher.
Le premier truc a faire, a mon avis, c'est de voir si tu part sur l'option a) ou la b) [je pense que les deux méthodes sont approximativement de même longueur et complexité]

[zygomatique]

salut

soit p cet entier

il existe n tel que n! =< p < (n + 1)!

donc on a la division euclidienne p = q.n! + r avec 0 =< r < n!

puis tu recommences avec r

....

[vizcaronbis]

Donne l'énoncé exact

Pour tout entier n, la somme des nombres k.k!, k de 0 à n est l'entier précèdant (n+1)!
Montrer que tout entier naturel n s'écrit d'une unique façon sous la forme n =;) akk!
k;)1

, chaque chiffre ak parcourant [0..k]

Il nous faut une réponse sous forme mathématiques, nous n'avons pas réussi à trouver, d'autres indices ?

[Ben314]

Par exemple en utilisant la méthode b) (que j'ai tendance à préférer et aussi pour que ce ne soit pas la même chose que ce que zygomatique t'a suggéré) :

On cherche et tels que .
Or sont tous divisible par 2 donc et, vu qu'on doit prendre la seule possibilité est de prendre pour le reste de la division de par 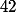et donc pour le quotient de cette même division.

Il reste à trouver et tels que .
Or sont tous divisible par 3 donc et, vu qu'on doit prendre la seule possibilité est de prendre pour le reste de la division de par 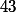et donc pour le quotient de cette même division.

Il reste à trouver et tels que .
Etc...

Et à travers ce processus, on tombera forcément sur un vu que, si alors .

On peut évidement faire le même type de raisonnement en "partant du haut" et ça risque d'être ce qui est attendu vu que dans la preuve ça dessus, on n'utilise pas la relation démontré précédemment (on en a pas besoin et c'est une des raisons pour lesquelles on préfère souvent partir "par le bas" pour trouver l'écriture d'un entier donné dans une base donnée)

BILAN : c'est très exactement la même chose que pour trouver par exemple l'écriture en base 10 d'un nombre entier...