Croissances comparées, dérivée n-ème
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Avr 2009, 20:53
par Nightmare » 09 Avr 2009, 20:53
Bonsoir :happy3:
Voici un exercice amusant posé à l'X :
Soit
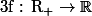
de classe

.
On suppose que pour tout

:
}(x)=\lim_{x\to +\infty} x^{\gamma}f(x)=0)
Montrer que
}(x)=0)
Bon courage (il n'est pas difficile)
:happy3:
-
Clise
- Membre Relatif
- Messages: 221
- Enregistré le: 16 Mai 2008, 20:59
-
 par Clise » 10 Avr 2009, 22:35
par Clise » 10 Avr 2009, 22:35
Bonsoir,
Je pense avoir eu une idée...
On a, par hypothèse pour une fonction
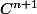
}(x)=\lim_{x\to +\infty} x^{\gamma}f(x)=0)
Comme f est
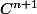
, la dérivée de f existe et est
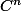
. On applique la même hypothèse et on a
=\lim_{x\to +\infty} x^{\gamma}f'(x)=0)
Et ainsi de suite par récurrence, on a

avec

qui existe et est

, d'où
=\lim_{x\to +\infty} x^{\gamma}f^{p}(x)=0)
On a donc prouvé que
}(x)=0)
Alors, ça marche ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Avr 2009, 22:49
par Nightmare » 10 Avr 2009, 22:49
Je ne vois pas pourquoi la dérivée de f vérifierait les hypothèses !
-
Clise
- Membre Relatif
- Messages: 221
- Enregistré le: 16 Mai 2008, 20:59
-
 par Clise » 10 Avr 2009, 23:32
par Clise » 10 Avr 2009, 23:32
oui tu as raison, je me suis un peu précipité, toutes les fonctions
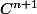
n'ont pas cette propriété ... :marteau:
Mais à part la récurrence, je n'ai pas d'autres idées :mur:
Je vais continuer à chercher :we:
-
Pafapafadidel
- Membre Naturel
- Messages: 87
- Enregistré le: 30 Mar 2009, 16:38
-
 par Pafapafadidel » 14 Avr 2009, 12:51
par Pafapafadidel » 14 Avr 2009, 12:51
J'ai trouvé qqchose mais je n'utilise pas toutes les hypothèses donc c'est surement faux...
Si une fonction

tends vers 0 a l'infini, sa dérivée existe et est intégrable à l'infini, donc elle tend vers 0 à l'infini, on a donc
=0 \Rightarrow \lim_{x \to + \infty} f'(x)=0)
.
Ainsi, pour tout

, on a
=0 \Rightarrow \lim_{x \to + \infty} (x^\gamma f(x))'=0)
, or
)'=x^\gamma f'(x) + \gamma x^{\gamma-1} f(x))
. A l'infini, on a
\leq x^\gamma f(x))
, donc
=0)
; de plus on sait que
)'=0)
, d'ou
=0)
.
En répétant cette manip autant de fois qu'il est nécessaire, on obtient le résultat demandé. Le problème est que je n'utilise pas l'hypothese
}(x)=0)
. Ou est l'erreur?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Avr 2009, 14:06
par Nightmare » 14 Avr 2009, 14:06
Pafapafadidel a écrit:Si une fonction

tends vers 0 a l'infini, sa dérivée existe et est intégrable à l'infini, donc elle tend vers 0 à l'infini, on a donc
=0 \Rightarrow \lim_{x \to + \infty} f'(x)=0)
Ca reste à prouver...
A l'infini, on a
\leq x^\gamma f(x))
Ou est l'erreur?
Ce n'est pas vrai pour tout gamma !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Avr 2009, 14:20
par yos » 14 Avr 2009, 14:20
Pafapafadidel a écrit:=0 \Rightarrow \lim_{x \to + \infty} f'(x)=0)
En général c'est faux. Prends un sinus amorti.
Pour l'exo, j'aurais envie de poser g(x)=f(1/x), g(0)=0... Mais j'ai pas regardé de très près.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Avr 2009, 11:15
par Nightmare » 15 Avr 2009, 11:15
Salut Yos :happy3:
As-tu avancé? Je n'ai pas abouti par ta méthode (qui n'est pas la même que la mienne) donc ça m'intéresserait de savoir si tu es arrivé à un résultat !
Personnellement j'y suis allé en utilisant un développement de Taylor (Laplace ou Lagrange)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
de classe
.
:
de classe
.
: